こんにちは、あすなろスタッフのカワイです!
今回は、連立方程式とは何かという事について、例を挙げつつ解説していきたいと思います。やりかたについてしっかり覚える必要はありませんので、気楽に読み進めていって下さい!
連立方程式って何だろう?解くってなに?と思っている方は、これを読んで大方理解してもらえるかなと思います!では、解説していきます!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校2年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
連立方程式とは?
連立方程式とは、2つ以上の方程式を組み合わせたもののことを言います。特に、今回からの数学で習う連立方程式では、2元1次方程式について扱っていくことになります。
(新しい単語を次々と出してしまってごめんなさい。)
2元1次方程式とは何かといいますと、式中に次数が1の文字が2種類ある方程式の事を言います。言葉で説明しても分かりづらいと思うので、例を挙げさせてください!
「次数ってなんだろう?」という場合は、こちらの記事で復習してみてください!【中2数学】単項式と多項式の違い、次数について解説します!
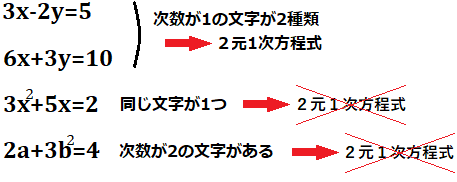
上の2式が2元1次方程式です!説明の通り、\(x\)と\(y\)の2種類の文字があり、どちらの文字も指数がついていないので、次数が1となっています。
上から3つ目の式は、文字の種類が1つだけであり、次数も2のものがあるので、2元1次方程式ではありません。
一番下の式も次数が2となっている文字があるので、2元1次方程式ではありません。
理解していただけたでしょうか?
大事な部分をお伝えしたところで、「これ実際どういう場面で使えるの?」という事について、やっと解説していきます。
例題.鉛筆と消しゴムの値段
1本x円の鉛筆と、1個y円の消しゴムを売っている店があります。
Aさんは3本の鉛筆と2個の消しゴムを買うと、合計で400円でした。
Bさんは4本の鉛筆と2個の消しゴムを買うと、合計で500円でした。
鉛筆と消しゴムの値段はいくらでしょうか?
このような問題で、連立方程式を用いることが出来ます!まず、図で表してみましょう。
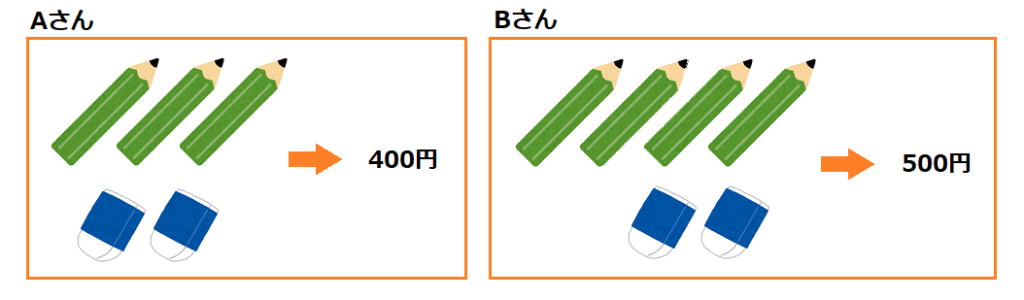
Aさんは、\(3\)つの鉛筆と\(2\)つの消しゴムを買うと、\(400\)円になりました。これを式に表すことを考えてみます。
まず、鉛筆3本の金額は、\(3\)(本)×\(x\)(円)となるので、\(3x\)円となりますね。
同様に、消しゴム\(2\)つの金額は、\(2\)(個)×\(y\)(円)となるので、\(2y\)円となります。
そして、問題文から、鉛筆\(3\)本と消しゴム\(2\)個の金額が\(400\)円となるとあるので、これを表してみると、

という形で表現できます!
同様に、Bさんも鉛筆\(4\)本と消しゴム\(1\)個の金額が\(500\)円となるので、これを式で表すと、

となります。
ここまでついてこれていますか…?
さて、2つの式をつくることが出来ました!
この式を連立させて書くと、
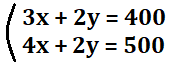
となります。このような形で表現したものを連立方程式といいます!
では、これらから、鉛筆\(x\)円と消しゴム\(y\)円の値段を計算していきましょう!
連立方程式では、計算を行う手法の一つに加減法があります。これについては、次回詳しく説明しますが、下のように計算を行っていきます。
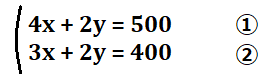
式2つに分かりやすいように番号を付けました。上と下の式では、\(y\)の項の係数が同じ(どちらも2)なので、①の式から②の式を引くことで、うまいこと\(y\)が消えてくれそうです。
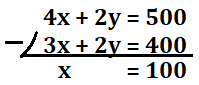
従って、上のように筆算の形にして、縦で計算を行います。筆算では、下の3式を計算しています。
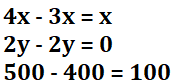
もしこれでもよく分からないという人は、下の図を見てください!
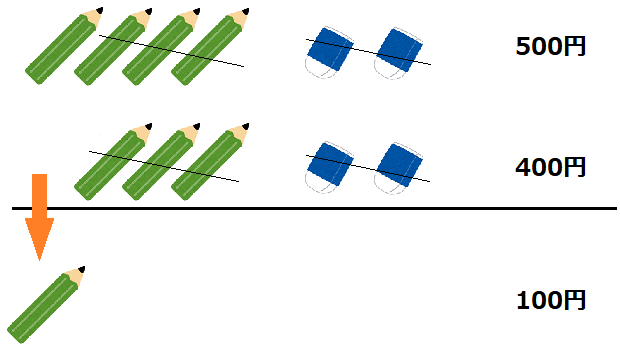
式をそのまま図に置き換えただけですが、合計の差額とものの数の差を見ると、鉛筆1つが残って、差額が\(100\)円という事が分かります。
さて、\(x=100\)なので、鉛筆1本の値段は\(100\)円となります!
ここから、消しゴムの値段を知るには、①か②の式に求めた\(x\)の値を代入すれば大丈夫です。\(x\)の値を式を連立させて解いた時点で、どちらの式に入れても\(y\)の値は等しくなります。
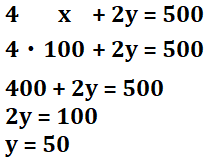
よって、消しゴム1個の値段は\(50\)円となります。
よって、この連立方程式の解は
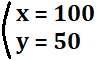
となります。
ところで、方程式の答えの事を解と言います。非常によく出てくる用語なので、覚えておくようにしましょう!
まとめ
いかがでしたか?連立方程式を解く流れを紹介していきました。詳しくは別の記事で解説していきますので、よかったら見てみて下さい!
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。