こんにちは、あすなろスタッフのカワイです。
今回は、前回勉強した比例を用いて、比例のグラフを作成していこうと思います。
グラフを用いて何か意味があるの?と思うかもしれません。しかし、グラフは目で大体の情報を抜き取ったり、比較したりすることができるという意味で重要なものです。
では、今回も解説していきます!
関連記事:【中1数学】比例ってなんだろう?どういう時に必要になるのか、解説します!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
小学校のおさらい
1本100円の鉛筆があります。本数と合計金額の関係をグラフに表してみよう。
この問題は、問題の設定をもとにグラフを作成することが目標です。
手順はこの通りです。
- 問題から式をつくる
- 式から表を作成する
- 表の値をグラフに置く
では、まずこの関係を式で表してみましょう。
何本買っても1本あたりの鉛筆の価格は変わらないので、比例定数は100(円)として良さそうです。
本数を\(x\)(本)、合計金額を\(y\)(円)とすると、この式は
$$y=100x$$
と書くことができます(ただし、本数はマイナスにはならないので、\(x≧0\))。
では、これを基に、表を作成してみましょう。
| \(x\):本数(本) | 0 | 1 | 2 | 3 | 4 | 5 | … | 8 |
| \(y\):合計金額(円) | 0 | 100 | 200 | 300 | 400 | 500 | … | 800 |
このような形になりますね。これは\(x\)に値を入れたときの計算結果(\(y\))の値をぞれぞれ上下で入れてあげれば、上のように作成できます!
では、これをグラフに置いてみましょう。
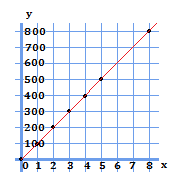
表に入れた部分について、対応する部分に点を打つとこうなります。
図より、これらの点は0を通る一直線を描くことができることが分かりました。
と、ここまでは小学6年生の頃の復習です!!何となく覚えているでしょうか?もし怪しいな…と思ったら復習をして次に進みましょう。
ここでいくつか新しい言葉を導入していきます。
横軸:\(x\)軸
横軸:\(y\)軸
\(x\)軸と\(y\)軸を合わせた呼び方:座標軸
\(x\)軸と\(y\)軸の交わる点(\(x\)と\(y\)の値がどちらも0の点):原点
では、中学の内容に入っていきましょう。
例.進む時間と位置の関係
人がある一方向に1時間に2kmの速さで止まらずに歩いています。0kmの地点を通った時間を0として、この人の進んだ時間と位置の関係をグラフに表してみよう。
問題のとおり、止まることなく1時間に2km進むということなので、2時間で4km、3時間だと…という風に予測することができそうです。
これだけでは小学校で習った問題と変わりません。これはもう中学生の勉強なので、マイナスの考え方を導入してみましょう。
この人は止まらずに歩き続けているという事なので、時間をはかり始める前も同様に歩いていたと考えてみましょう。
すると、1時間前は0の2km前の地点にいると考えることができませんか?同様に、2時間前は?3時間前は?と知ることができそうです。
さて、この関係を式にしてみましょう。時間が一定なので、これが比例定数としましょう。時間を\(x\)(時間)、そのときの位置を\(y\)(km)とすると、式は
$$y=2x$$
とおくことができます。
では、これを基に、表を作成してみましょう。
| \(x\):時間 | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| \(y\):位置 | … | -6 | -4 | -2 | 0 | 2 | 4 | 6 | … |
この表をグラフに置いてみましょう。
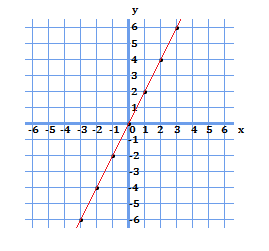
マイナスが含まれたので、グラフの表示域が拡大しました。
このグラフでも同様に原点を通り、全ての点が一直線上にあることが分かります。
そして、1や2などの整数で表される時間以外の値も、グラフから読み取ることができます。
例えば、0と1時間の間(0.5時間)の時にどこにいるのかな…と考えた時に、
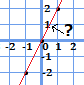
\(y\)軸の1と交差している部分かな?と大体推測することができます。これを実際に式より計算してみると、
$$y=2×0.5$$
$$y=1$$
より、確かにこの\(x=0.5\)(時間)に対応する\(y\)は\(1\)(km)だと分かりました。
グラフを使うと、計算をせずに大まかな予測を目で見て確認することができます。
今度は、この人が進む速さを1時間に3kmとしてみましょう。
上と同様に考えると、式は
$$y=3x$$
となり、これをグラフに表すと、
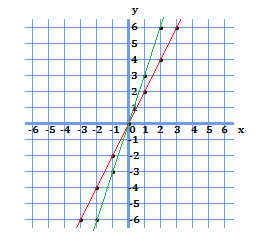
こうなりました。緑で書いたのが\(y=3x\)、赤で書いたのが例で示した\(y=2x\)となります。
この2つのグラフの違いは何でしょうか?
そうです、グラフの傾きが異なります。
\(y=3x\)のグラフの方が傾きが急になっていることが見て分かりますね。従って、比例定数が大きいほど、グラフの傾きが急になるということが分かります。
逆に同じ部分はどこかというと、どちらも原点を通っています。それは式の\(y\)か\(x\)に0を入れると、式の計算より、もう一方が0になることから分かりますね。
今回はここまでです!
まとめ
グラフの書き方
- 問題から式をつくる
- 式から表を作成する
- 表の値をグラフに置く
比例の関数のグラフの特徴(比例定数が正の場合)
- 原点を通り、右上から左下までの一直線となる
- 比例定数が大きいほど傾きが急になる
いかがでしたか?比例の問題からグラフを作成する方法を解説しました。
次回は、比例定数が負の場合の場合、グラフはどうなるのか?について解説していきます。