こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、”2次方程式って一体何の為の計算なのか分からない!”という人に向けて、
具体例を通して理解してもらえるように解説したいと思います!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。
図形の辺の長さを解く(その1)
2次方程式の利用例の1つとして、長方形の辺の長さを知ることが出来ます。
下の図を見てみましょう。
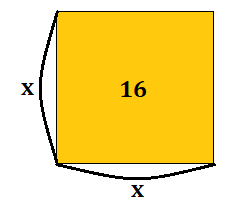
面積が\(16\)であると分かっていて、辺の長さは分からないけど長さは等しいと分かっている図形があります。
上のような図形の面積と辺の関係式は 縦×横=面積 となりますね。
今回、縦も横も\(x\)と表されるので、式は\(x×x=x^{2}=16\)となります。
分かりやすい解き方として、\(x\)に適当な数字を1から順に入れてみましょう。
| 辺の長さ\(x\) | \(1\) | \(2\) | \(3\) | \(4\) | … |
| 面積 | \(1\) | \(4\) | \(9\) | \(16\) | … |
\(x=4\)のときに、面積が丁度\(16\)となったので、辺の長さは\(4\)で間違いなさそうです。
表を用いて解きましたが、平方根を取ることで解くことも可能です!
\(x^{2}=16\)
より、
\(x=±\sqrt{16}\)
となりますね。
\(16\)は\(4×4\)なので、\(x=±4\)すなわち\(x=4,x=-4\)となります。
求める数は正の数である必要があるので、\(x≠-4\)すなわち\(x=-4\)は答えに適しません。
従って、\(x=4\)となり、辺の長さは\(4\)になります。
このように、上の表と同様に解くことが出来ました。
図形の辺の長さを解く(その2)
上の問題を解いたうえで、今度は下の図の問題を見ていきましょう。
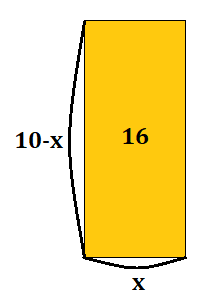
今度も面積は\(16\)ですが、辺のそれぞれに変数があり、一目ではよく分からない状態になっています。
図に倣って、縦を\(10-x\)、横を\(x\)とすると 縦×横=面積 より、
\((10-x)x=16\)
となります。先程と同様に\(x\)に値を入れていけば、近い値まで持って行くことが出来そうです。
\(x=1\)を入れると、\((10-1)×1=9\)
といった形で計算することができますね。これを一旦\(x=9\)まで解いて、表を作成してみましょう。
| \(x\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) | \(8\) | \(9\) |
| 面積 | \(9\) | \(16\) | \(21\) | \(24\) | \(25\) | \(24\) | \(21\) | \(16\) | \(9\) |
正しい面積は\(16\)で、\(x\)が\(2\)のときと、\(8\)のときに求めたい面積の値である\(16\)となりました。
値が2つ…?と思うかもしれませんが、間違いではありません。
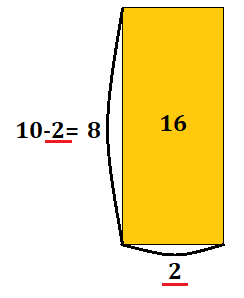
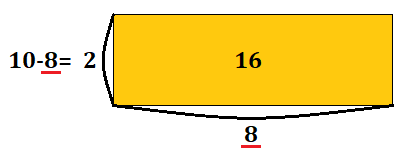
赤線で引いたところが\(x\)となっています。
縦が\(2\)のときは横が\(8\)、縦が\(8\)のときは横が\(2\)となる為、2パターン考えられるのです。
従って、\(x=2\)と\(x=8\)となります。
\((10-x)x=16\)は\(x^{2}-10x+16=0\)という形に書き換えることができ、
これは確かに2次方程式であると分かります。
2次方程式の場合、基本的に解が2つあるので、1つだけ見つけて満足せずに、2つ見つけるようにしましょう。
まとめ
いかがだったでしょうか。2次方程式を解くと、解が2つ出てきます。
より詳しい解き方は別の記事で紹介するので、良かったら見てみて下さいね!
やってみよう!
次の\(x\)を求めてみよう。
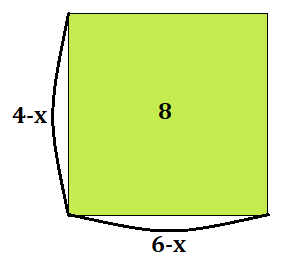
こたえ
\(x=2,x=8\)
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。