こんにちは。あすなろスタッフのカワイです。
今回は、負の数を含めた足し算について解説していきます!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
加法とは?
小学校の頃まで足し算と言ってきた言葉ですが、中学数学から「加法」といいます。また、加法の答えを「和」といいます。どちらもよく使われるので、覚えておきましょう!
また、式に含まれる要素(例えば、3+4であれば3,4)の事を「項」といいます。加法だけでなく、様々な式でよく使われる言葉になるので、頭に入れておいてくださいね。
加法というのは小学校でやってきた足し算の延長線になるのですが、負の数が入ってくると、少し複雑になってしまいます。ですが、これも数直線を使って考えれば、目で見て考えられるので、そこまで構えなくても大丈夫です!
例題1 小学校で習った足し算
例題として、まず(+2)+(+3)を数直線を使って考えてみましょう。
まず、+を右に進む方向、-を左に進む方向とでもします。

\(0\)をスタート地点とすると、\(+2\)というのは右に\(2\)進む方向となるので\(+2\)になります。そこからさらに\(+3\)するということは、右に\(3\)進む方向にいくということなります。この2つの操作の結果、右に\(+5\)進んでいることになります。すなわち、和は\(+5\)です。
小学校でたくさんやった計算だとので、答えは数直線を使わなくても解けたのではないかと思いますが、加法というのはこのような数直線を使って考えることができます。
では、次は負の数を含んだ式の計算を数直線を用いて考えていきましょう。
例題2 正の数-負の数
次は、
\((+3)+(-5)\)
を計算してみましょう。上の例と同様に、数直線を使って考えていきます。

\(0\)をスタート地点として、まず\(+3\)するので、\(0\)から右に\(3\)進みました。次は\(-5\)なので、左へ\(5\)進む方向に行くことになります。その結果をみると、左に\(2\)進んでいることになります。すなわち、この和は\(-2\)となります。
足し算をしているはずなのに、和が負の値になってしまいました。足しているのに答えが0よりも小さい値になってしまったということです。小学校までの足し算と違うことが起こっているので「何故足し算なのに数字が減っているの?」と思う人もいるかもしれません。
ですが、よく考えてみてください。小学校までの足し算では、数直線での考え方でいう右に進むすなわち値が増える場合しか考えてこなかったので、足し算で答えが負になることが無かっただけなのです。
中学からの加法(足し算)では、数直線上での考え方で言う右に進むだけでなく左に進むというパターンも登場したということになります。だから、値が減ることは不思議なことではないのです。
この際に、物の数を増やしたり減らしたりという考え方をしてしまうと、中々理解しづらくなるかと思います。なので、温度計やお金の増減など負の数が存在するもので考えてみてください。
例題3 負の数+負の数
最後に、\((-1)+(-4)\)を計算してみましょう。
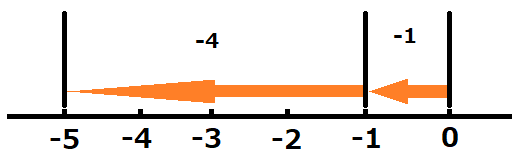
\(0\)をスタートとしたときに、まず\(-1\)なので、左に\(1\)進む方向に進みます。次に、\(-4\)足されているので、左に\(4\)進む方向に進みます。
結果左に\(5\)進んでいるので、和は\(-5\)となります。
この式では一度も右へ進むことはありませんでしたが、値を変える操作を加えているいう意味で加法と考えられます。
式による計算判断方法
ここまで数直線を用いて考え方を解説してきましたが、毎回数直線を書いて考えていたら時間が掛かってしまって現実的ではありません。
そこで、ここからは式を見ただけで計算できる方法について簡単に解説していきます(今回は二つの値の加法に限定します。)
同符号同士の加法の場合
同符号同士の加法であれば、絶対値を足し算して符号をつけるというやり方で求められます。
例えば、例1で考えた\((+2)+(+3)\)について式を見て計算してみましょう。2つの値はどちらも正の数なので、絶対値の足し算をしていきます。
\(2+3=5\)より絶対値の和は\(5\)であるとわかります。最後に、足し合わせた2つの値はどちらも正なので、この和は\(+5\)であるとわかります。
次に、例3で考えた\((-1)+(-4)\)について式を見て計算してみましょう。2つの値はどちらも負の数なので、絶対値の足し算をしていきます。
\(1+4=5\)より、絶対値の和は\(5\)であるとわかります。足し合わせた2つの値はどちらも負なので、絶対値の和に負の符号をつけて、答えは\(-5\)となります。
異符号の加法の場合
異符号の加法の場合は、
- 「絶対値の大きい方」ー「絶対値の小さい方」をする
- 絶対値の大きい方についていた符号をつける
で答えを出すことができます。
例として、例2で求めた \((+3)+(-5)\)について考えてみましょう。
まず、\(+3\)と\(-5\)の絶対値を比べていきます。それぞれの絶対値である\(3\)と\(5\)では\(5\)の方が大きいとわかりますね。なので、\(5\)から\(3\)を引くと、\(5-3=2\)となります。
大きい方の絶対値である\(5\)は、符号を考えると\(-5\)なので、上で求めた値に−をつけて\(-2\)としたものが和となります。
まとめ
- 同じ符号同士の加法
$$(+2)+(+3)=+(2+3)=+5$$
$$(-1)+(-4)=-(1+4)=-5$$
符号を前に着けて、絶対値の足し算をする
- 異なる符号の加法
$$(+3)+(-5)=-(-3+5)=-2$$
絶対値の大きい方から絶対値の小さいほうを引いて、大きい方の符号をつける
やってみよう!
次の式の和を求めましょう 。
- $$(+6)+(-3)$$
- $$(-1)+(-2)$$
- $$(-4)+(+3)$$
- $$(-2)+(-2)$$
答え
- \((+6)+(-3)=+3\)
【解説】異符号なので、絶対値の大きい\(6\)から絶対値の小さい\(3\)を引いた\(3\)が絶対値。\(6\)は正の数なので、答えは正となる。 - \((-1)+(-2)=-3\)
【解説】同符号なので、絶対値同士を足し合わせると\(1+2=3\)となる。どちらも負の数なので、答えも負となる。 - \((-4)+(+3)=-1\)
【解説】異符号なので、絶対値の大きい\(4\)から絶対値の小さい\(3\)を引いた\(1\)が絶対値。絶対値が大きいほうの\(-4\)は負の数なので、答えは負となる。 - \((-2)+(-2)=-4\)
【解説】同符号なので、絶対値を足し合わせると\(2+2=4\)となる。どちらも負の数なので、答えは負となる。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。