こんにちは、あすなろスタッフのカワイです!
今回から、方程式の解説を行っていきたいと思います!
「方程式」という名前から、何となく難しそうだな、と思う方もいるかもしれませんが、言葉の響きほど難しいものではありません!
一つ一つ確認しながら学んでいけば、必ず方程式を解くことができるようになります!では、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
方程式とは…?
「\(x\)や\(y\)などの文字を含むある式が、等式で結ばれたもの」のことを方程式といいます。(厳密には意味が異なりますが、今のところこの解釈で大丈夫です)
ちょっと何を言っているか分からないですよね。。。
そもそも、等式ってなんでしょうか?
等式とは左辺と右辺が等しい式のことをいいます。天秤に例えると、右と左が釣り合っている状態ということですね。
これを分かりやすくするために、天秤を使ったゲームをやって等式を理解してみましょう。
天秤を使ったゲームで等式を理解しよう!
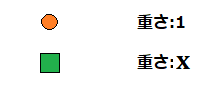
このような2種類のものがあります。〇は重さが\(1\)で、□は重さが分かりませんが、\(x\)で表すことができるとします。〇の重さが分かっているので、これらを天秤に置いて、何とか□の重さを知ることができないでしょうか。
まず、左に〇を\(3\)つのせて、右に□を\(2\)つのせてみます。
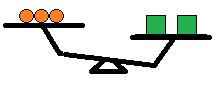
すると、こんな具合になりました。〇\(3\)つよりも□\(2\)つの方が重いようです。
次に、左の〇を\(5\)つに変えてみます。
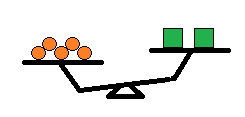
すると、今度は〇を置いた側の方が重くなりました。
上の2つから、□\(2\)つは\(3\)より重く、\(5\)より軽いということが分かったので、次は〇を\(4\)つにしてみましょう。
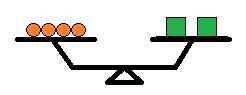
すると、ここで釣り合いました。釣り合ったということは、右の重さと左の重さが同じということです。これを式に表してみましょう。
重さ\(1\)の〇\(4\)つと、重さ\(x\)の□\(2\)つが釣り合っていることから、
$$1×4=x×2$$
$$2x=4$$
と書くことが出来ます!ここで、\(2x=4\)という式は、右と左が等しいことから等式と呼びます。またこれは文字を含んだ式がイコール(\(=\))で結ばれているので方程式といえます。
さて、式は出来ましたが、肝心の□の重さはまだ求められていませんね。これを見つけてみましょう。
$$2x=4$$
両辺を2で割って、
$$x=2$$
となりました。したがって、□の重さは\(2\)であると分かりました!
このように式が成立するような文字の値を、方程式の解といいます。
では、この\(x\)に他の値を入れても、この数式は成り立つでしょうか?
・
・
・
いえ、成り立ちません。方程式の解は、1年生での学習範囲では、1つの値しかとりません。(1次方程式の解は1つに定められます。)
ですから、このように式を用いて、ある1つの分からないパラメータ(重さ・速さ・個数など)を一意に決定することが出来ます!
まとめ
方程式を用いることで、分からない重さや長さ、個数などを知ることができます!今後の記事では等式の性質・方程式の計算などを解説していきますが、自分のペースでゆっくり理解してもらえたらOKです!
最後までご覧いただきありがとうございました!
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。