こんにちは、あすなろスタッフのカワイです。
確率については前に別記事で説明しましたが、円の図や計算を用いた説明がほとんどだったので、分かりにくかったかもしれません。
”ちょっと計算で確率を導くのは難しくて抵抗があるな…”という人や、”確率問題のミスを減らしたいな…”という人に向けた最適な方法として、「樹形図」があります!
今回は、確率とは何かということについて振り返りながら、この樹形図の意味、解き方まで詳しく解説していきます!
では、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
【おさらい】確率ってなんだっけ?
樹形図に入る前に、確率とは何なのかを振り返っていきましょう。
確率とは、
偶然起こるすべての現象を1としたとき、あることがらの期待される程度を数字で表したもの
と考えます。
より具体的に説明すると、
”ありうる全てのパターンのうち、何回特定の条件のパターンが登場するか」ということを表したもの”
となります。これを公式で表すとき、
\(確率=\frac{○○という事象が起こる数}{事象のすべての数}\)
という形で示されます。
より詳しく「確率」とは何か?について知りたい人は、別記事を読んでみて下さい。
関連記事:【中2数学】確率ってなんだろう?その意味と身近な例を紹介します!
樹形図を使って確率を解いてみよう!
簡単な確率を考えるうえで有用な手法として樹形図があります!
樹形図とは、名前の通り、可能性のある事象を樹の枝のように伸ばしていって、すべての事象(パターン)について視覚的に確認する手法です。
このようなことから、起こる事象が多いものについては、時間がかかったり、逆にミスが増えてしまう可能性があり、あまり使うメリットは無いかもしれません。
しかし、中学で勉強する確率は、事象の数が少ない場合がほとんどなので、時間もかからず、多くの場面で有用な手法となります!
前置きはこの辺にして、早速例題をもとにやり方を解説していきますね!
もし手元に鉛筆と適当な紙があれば、一緒に手を動かして書いてみましょう。
例1.コインの表裏
”1つのコインを3回投げた時、表が2回、裏が1回出る確率を求めてみよう。(表と裏が出る順番は考えないとし、コインは同様に確からしいとする。)”
樹形図では、おこる順番に従って書いていきます。
したがって、まず、1回目の時のコインで起こることを書きます。〇を表、●を裏としましょう。

まず、表と裏の2パターンだけですね。(コインの表面に対してコインの厚みの部分は十分に小さいので、コインが表でも裏でもない可能性は0とします)
上の図のように、縦に並べて書きます。この時に、2回目以降の可能性を書いていくことが出来るように、上下のスペースをかなり取っておきましょう!
次に、2回目の時のコインで起こることを書いていきます。
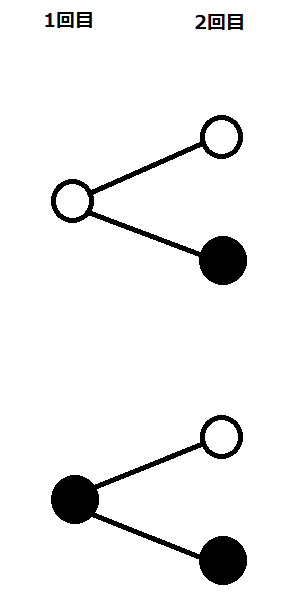
2回目も1回目と同様に、コインは表と裏の2パターンになりますが、1回目に起きたことの連続で考えると、
- 「1回目に表が出て、2回目に表が出た場合」
- 「1回目に表が出て、2回目の裏が出た場合」
- 「1回目に裏が出て、2回目に表が出た場合」
- 「1回目に裏が出て、2回目に裏が出た場合」
と考えられるので、計4パターンの可能性が考えられることになります。
回数を増やしていくと、どんどん可能性の幅が広がっていきます。なので、書くスペースを用意していなかった人は、今のうちに書き直しておきましょう。
さて、3回目はどうなるのかというと、
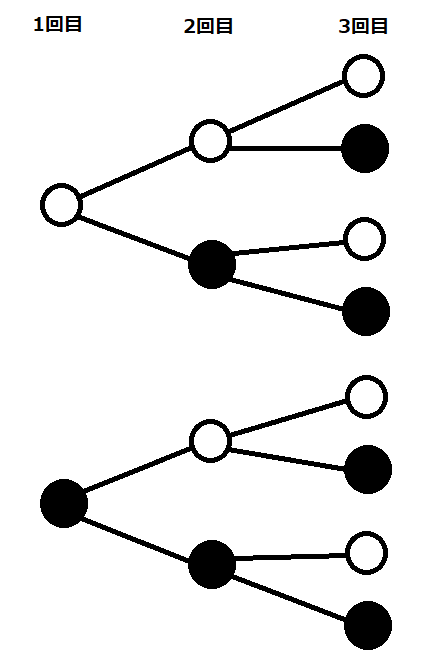
このようになりますね。2回目までの結果の4パターンに、さらに「表」と「裏」のパターンが追加されるので、計8パターンとなります。
さて、ここから、マークの数をそれぞれ数える事によって、全体でどのような場合分けができるのか、やってみましょう。
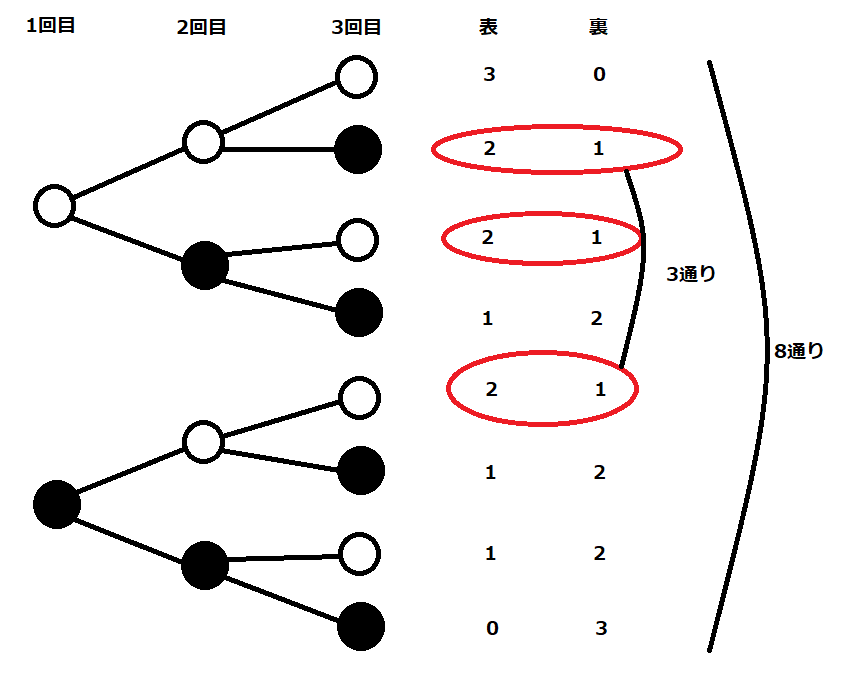
分かりやすいように、簡単な表にして考えてみました。
今回の問題は表が2回、裏が1回出る確率なので、そのパターンを樹形図から数えると、3パターンですね。
次に、全てのパターンを数えると、樹形図で数えると、8パターンです。
確率は\(\frac{表が2回、裏が1回となるパターン}{3回投げたときのすべてのパターン}\)
で計算することが出来るので、この確率は\(\frac{3}{8}\)となります!
樹形図を用いることで、自分が知りたい事象のおこる回数と、すべてのおこる回数が視覚的に確認することが出来る事を体感して頂けたでしょうか?
例2.じゃんけんの勝敗
”2人でじゃんけんを2回するとき、少なくとも1回(1回もしくは2回)はあいこになる確率を求めてみよう”
じゃんけんについても、コインと同じように樹形図を用いて考えることが出来ます。
勝ちを〇、あいこを△、負けを×として1回目のじゃんけんで起こるパターンを書いてみましょう。
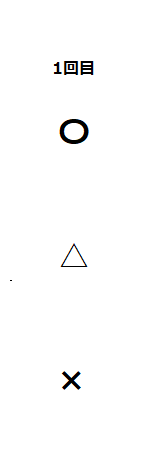
上のようになったでしょうか?
次に、2回目の結果を書いてみましょう。
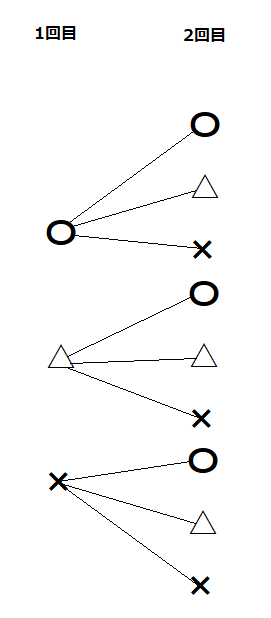
上のようになっていたら良いです!
書き終わったら、早速今回知りたいパターンについて考えていきましょう。
”あいこが少なくとも1回”なので、1回目もしくは2回目であいこになるパターンを探してみましょう。該当するものの隣に〇を付けていくと分かりやすいかもしれません。
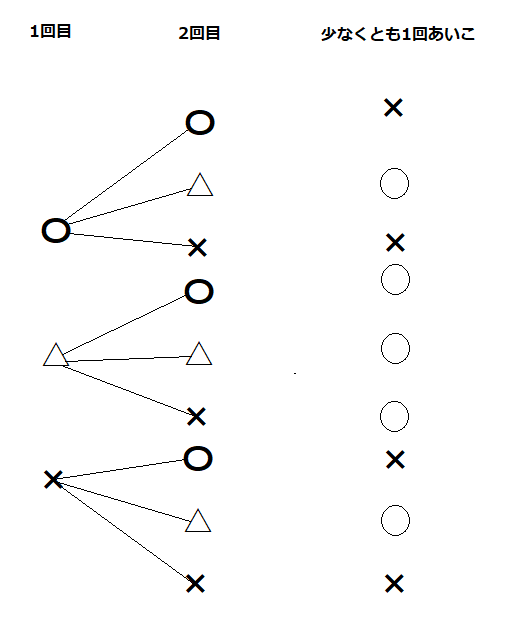
このようになりましたか?
あいこが起こっている回数は5回、すべての可能性を数えると9回になるので、
答えは\(\frac{5}{9}\)となります。
まとめ
- 樹形図は、起こる全ての事象(パターン)について書き出す手法である →視覚的にある事象の数と全ての事象の数を知ることが出来る
確率だけに限らず、数学を解くときにたいせつな事は、なるべく分かりやすい方法で考えるという事です。計算で手軽に進める力も非常に大切ではありますが、内容を理解しながら「目で見てわかる」方法を取って進めてことも、同じくらい大切な力です(特に中学数学では重要です!)。
確率はその重要性を特に感じやすい単元なので、是非「樹形図」を活用することによって、解ける楽しさを感じながら勉強を進めていきましょう!
やってみよう!
- 1枚のコインを3回投げた時、表が少なくとも2回(2回もしくは3回)出る確率を求めてみよう。(例1.を参考に)
- 2回じゃんけんしたとき、じゃんけんで1回勝ち、1回あいこになる確率を求めてみよう。(例2.を参考に)
答え
- \(\frac{1}{2}\)
【解説】例1の樹形図を確認すると、表が3回の場合が1通り、表が2回の場合が3通りとわかる。全部のパターンが8通りとなるので、答えは\(\frac{1}{2}\)となる。 - \(\frac{2}{9}\)
【解説】例2の樹形図を確認すると「1回目に勝ち、2回目にあいこ」の場合と「1回目にあいこ、2回目に勝ち」の2通りがある。全部のパターンが9通りとなるので、答えは\(\frac{2}{9}\)となる。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。