こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、一次関数によって表された図形の面積の求め方について解説していきたいと思います!
苦手に感じている人も多くいる問題だと思いますが、高校入試の問題に繋がってくる可能性が高いので、必ずマスターして抑えておくようにしましょう!
では、今回も頑張っていきましょう!
わからない…を“わかる!”に変える家庭教師
「勉強がわからない」そんな悩みは、あすなろ関西の家庭教師が解決!一人ひとりに合った勉強方法で、小学生から高校受験までサポート!
たった15分の勉強で、これまでの3倍の効果を実感!そんな効率的な学びを、無料体験で試してみませんか?

参照元:文部科学省 学習指導要領「生きる力」
=もくじ=
一次関数で表された図形の面積とは?
一次関数はグラフに表したときに直線となります。この一次関数が複数あると考えると、直線同士の交点や座標を使って図形が出来ることがあります。
解く方針としては、
- 直線の式を求める(直線の式が分からない場合)
- 直線同士の交点を求める
- 図形の面積を求める公式を用いて面積を求める
という流れになります。読む感じはやることが多そうですが、慣れてしまえば作業的に解くことが出来ます。
問題1
次の赤で塗られた部分の面積を求めてみよう。
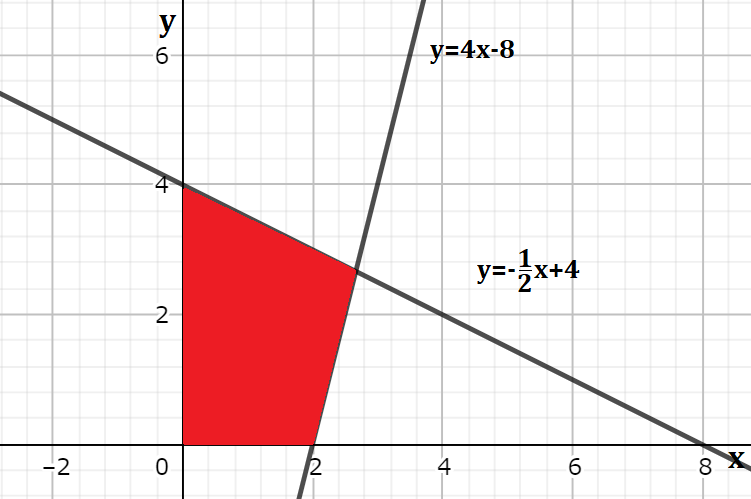
図を見ると、赤の部分は四角形になっていますが、台形の面積としてもとめるにしても、2つの一次関数の交点の部分が分からないと、高さを求めることが出来ないので、面積を求めることも出来なさそうです。
なので、上記の解く方針に従って、まずは直線の交点を求めていきましょう!
\(y=4x-8\)と\(y=-\frac{1}{2}x+4\)の交点を求めるには、これらの連立方程式を解けばOKです。何故連立方程式を解くかというと…
連立方程式というのは、2つの式に共通した変数の組み合わせ(ここでは\(x\)と\(y\))を求めるものです。共通する\(x\)と\(y\)はすなわち交点の事だからです。
さて、これを連立方程式にすると、
\begin{eqnarray}\left\{ \begin{array}{l}y=4x-8\\y=\frac{1}{2}x+4\end{array}\right.\end{eqnarray}
となります。
これについて解くと、
\(4x-8=-\frac{1}{2}x+4\)
\(8x-16=-x+8\)
\(9x=24\)
\(x=\frac{24}{9}=\frac{8}{3}\)
\(y=4×\frac{8}{3}-8\)
\(y=\frac{8}{3}\)
となります。
したがって、この交点は(\(\frac{8}{3},\frac{8}{3}\))であると分かりました。では、この点を用いて面積を求めていきましょう。
求め方はいくつかありますが、そのうち2つを用いて解いていこうと思います。
解法その1
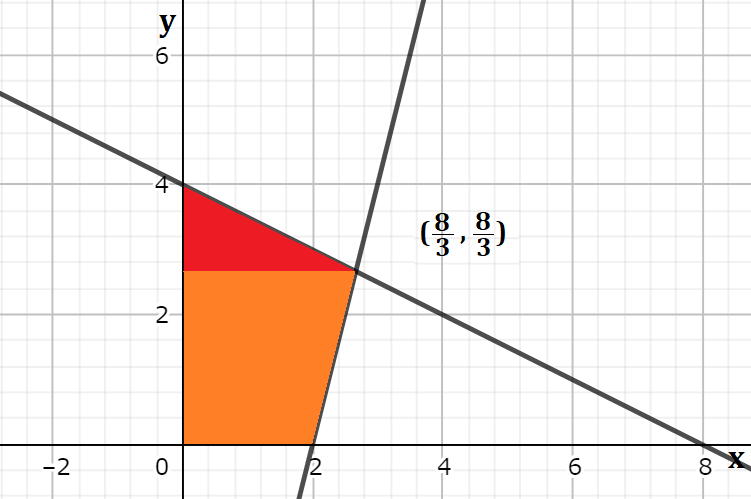
交点を\(x\)軸に対して平行に線を引いた時の上側(赤)と下側(オレンジ)の面積をそれぞれ求めて足す、という方針で求めていきましょう。
上側(赤)の面積は、\(y\)軸を底辺、交点から底辺までを高さとみると、三角形の面積の公式を使えそうです。
ここで注意する点は、
- 底辺は\(y\)軸に平行な長さだから、\(y\)座標の差で求める
- 高さは\(x\)軸に平行な長さだから、\(x\)座標の差で求める
という点に注意です!軸に平行な成分を使って長さを求めます。
文章が長くなってしまうので、困ったら図に戻って考えてみて下さい!
さて、座標から底辺の長さは
\(4-\frac{8}{3}=\frac{4}{3}\)
次に座標から高さの長さは
\(\frac{8}{3}-0=\frac{8}{3}\)
となります。
従って、上側(赤)の面積は、三角形の面積の公式より、
\(\frac{4}{3}×\frac{8}{3}÷2=\frac{16}{9}\)
となります。
次に、下側(オレンジ)の面積を求めていきますが、求めたい面積の図形は台形となっています。(台形の面積は「(上辺+下辺)×高さ÷2」で求められます。)
上辺の長さは上で求めた高さと同じなので、\(\frac{8}{3}\)
下辺の長さは、グラフより、\(2\)
高さは交点の\(y\)座標から\(y=0\)までの長さになるので、\(\frac{8}{3}\)
これを使って、台形の面積を求めると、
\((\frac{8}{3}+2)×\frac{8}{3}÷2=\frac{56}{9}\)
となります。
さて、上側(赤)と下側(オレンジ)を足し合わせると、
\(\frac{16}{9}+\frac{56}{9}=\frac{72}{9}=8\)
となります。
これで、求めたい面積が求まりました。


解法その2
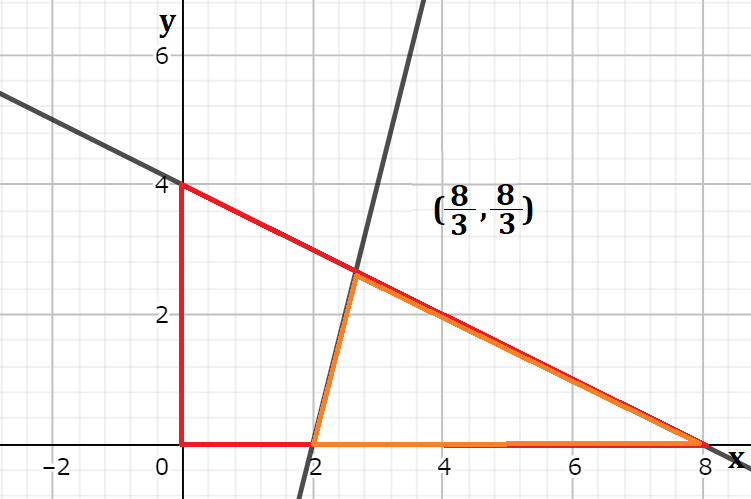
次は、大きい三角形(赤)から小さい三角形(オレンジ)の部分を引いた残りの部分が求めたい面積となるので、その方針で解いていきます。
大きい三角形(赤)はグラフより底辺が\(8\)で高さが\(4\)と見ることが出来るので、
この面積は、
\(8×4÷2=16\)
となります。
次に、小さい三角形(オレンジ)の底辺はグラフから読み取って\(8-2=6\)となり、
高さは交点から\(x\)軸までの最短距離となるので、\(\frac{8}{3}\)となります。
これを求めると、
\(6×\frac{8}{3}÷2=8\)
となります。
こちらの方法でも同様の答えを導くことが出来ました!
問題2
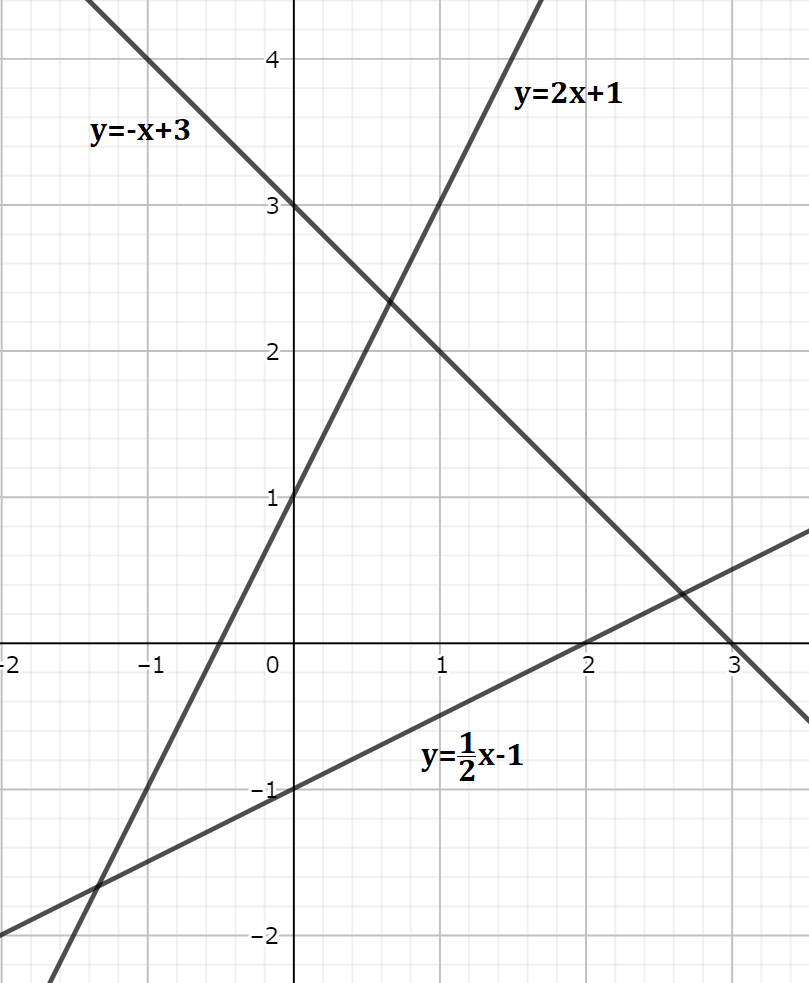
次は、この3つの線に囲まれた部分の面積について求めていきましょう。
今回の問題も、必要な座標を求めて、その後に面積を求めていくという方針で進めていきましょう。
交点の座標を求める!
まず、それぞれの交点を求めていきましょう。(求め方は、問題1の連立方程式と一緒です)
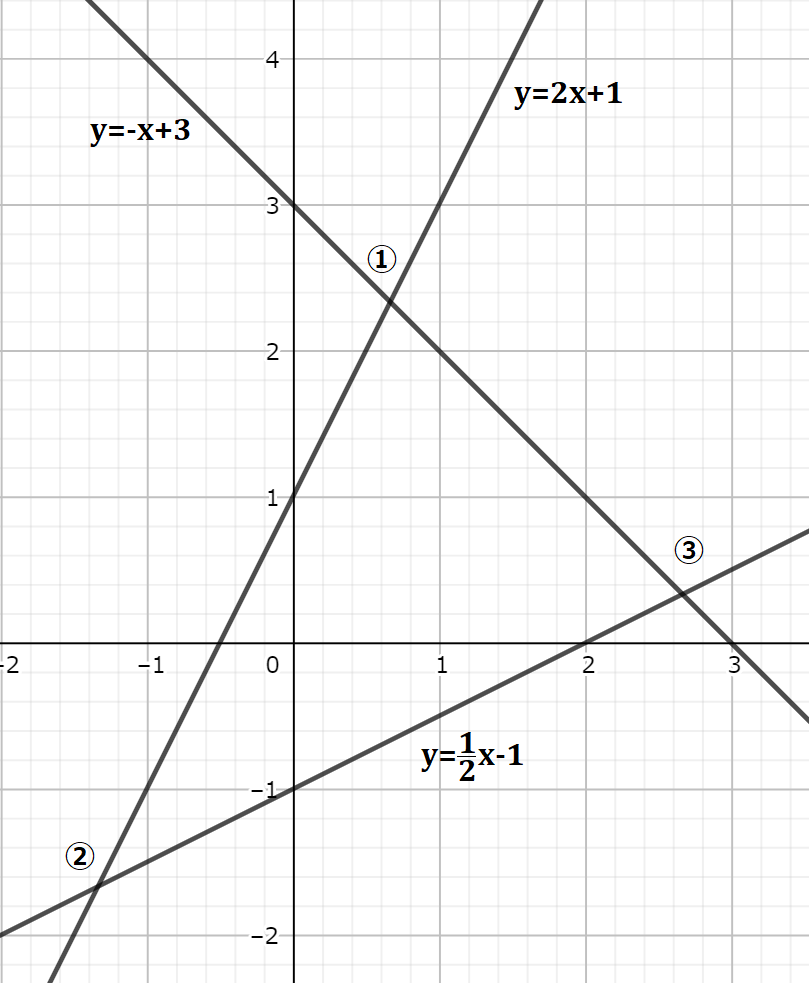
図のように、点をそれぞれ①〜③とします。
①は\(y=-x+3\)と\(y=2x+1\)の交点なので、
\(-x+3=2x+1\)
\(3x=2\)
\(x=\frac{2}{3}\)
\(y=2×\frac{2}{3}+1\)
\(y=\frac{7}{3}\)
より、①の座標は\((\frac{2}{3},\frac{7}{3})\)
と分かりました。
②は\(y=2x+1\)と\(y=\frac{1}{2}x-1\)の交点なので、
\(2x+1=\frac{1}{2}x-1\)
\(4x+2=x-2\)
\(3x=-4\)
\(x=-\frac{4}{3}\)
\(y=2×(-\frac{4}{3})+1\)
\(y=-\frac{5}{3}\)
より、②の座標は\((-\frac{4}{3},-\frac{5}{3})\)
と分かりました。
③は\(y=\frac{1}{2}x-1\)と\(y=-x+3\)の交点なので、
\(\frac{1}{2}x-1=-x+3\)
\(x-2=-2x+6\)
\(3x=8\)
\(x=\frac{8}{3}\)
\(y=-\frac{8}{3}+3\)
\(y=\frac{1}{3}\)
より、③の座標は\((\frac{8}{3},\frac{1}{3})\)
と分かりました。
面積を求める方針を決める!
では、3点が分かったので、3つの式で囲まれた面積を求めていきましょう。
考え方はいくつもありますが、
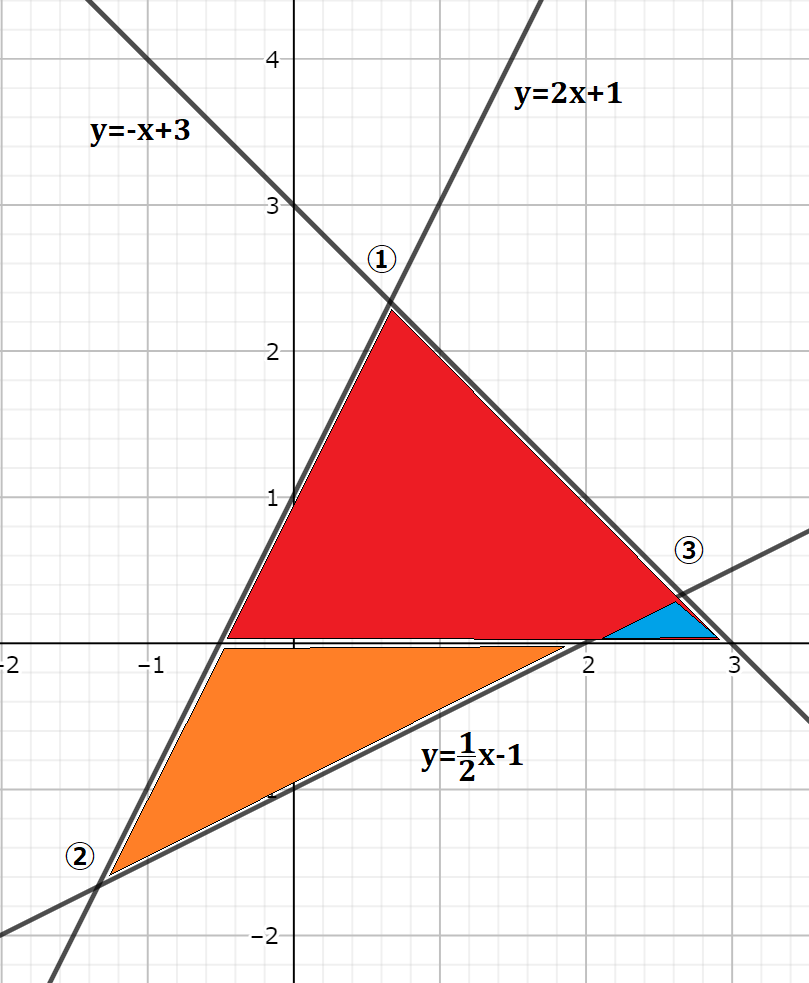
今回は、上側(赤)+下側(オレンジ)-余分の三角形(青)という方針で考えていきましょう。


分割した面積をそれぞれ求める!
まず、上側(赤)の三角形の底辺の長さを求めるために、\(x\)軸と\(2x+1\)の交点の座標を求めなくてはいけません。
\(0=2x+1\)
より、
\(x=-\frac{1}{2}\)
となり、この座標は\((-\frac{1}{2},0)\)
であると分かります。
従って、上側(赤)の三角形の底辺は、
\(3-(-\frac{1}{2})=\frac{7}{2}\)
となります。
次に、高さは①の\(y\)座標の値に等しいので、\(\frac{7}{3}\)
となります。
これより、上側(赤)の三角形の面積は、
\(\frac{7}{2}×\frac{7}{3}÷2=\frac{49}{12}\)
と分かりました。
次に下側(オレンジ)の三角形の面積を求めましょう。
底辺は、先程求めた交点を用いて、
\(2-(-\frac{1}{2})=\frac{5}{2}\)
であり、高さは、\(x\)軸と②の座標の\(y\)座標の最短距離となるので、\(\frac{5}{3}\)となります。
これを使って、下側(オレンジ)の三角形の面積を求めると、
\(\frac{5}{2}×\frac{5}{3}÷2=\frac{25}{12}\)
となりました。
この2つを足し合わせると、余分の三角形(青)の部分も含まれてしまって、囲った部分をはみ出してしまうので、ここを引きます。
底辺は\(3-2=1\)で、高さは③の\(y\)座標より\(\frac{1}{2}\)となるので、
余分の三角形(青)の面積は、
\(\frac{1}{2}\)
となります。
最後に、これらを足し引きすると、求めたい面積Sは
\(S=\frac{49}{12}+\frac{25}{12}-\frac{1}{2}\)
\(S=\frac{17}{3}\)
となります。
まとめ
今回は一次関数によって表された図形の面積の求め方を解説しました。
計算する箇所が多くミスをしやすいので、試験に出しやすい問題です。しっかり理解して勉強するようにしましょう。
また、問題1は面積を求める方針を2つ示しましたが、計算の手間や、しやすさが違ったと思います。今回の問題以外でも、大抵の問題はいくつかの解法があるので、より解きやすい方法を自分で見つける方法を探りながら、練習問題をいくつか解いてみて下さい。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
”やる気”と”自信”を育てる、あすなろ関西の学習サポート
どんな単元もコツをつかめば驚くほどスムーズに理解できるようになります! だからこそ、一人で悩み続ける必要はありません。
あすなろ関西は、「やる気づくり」や「できる喜び」を一番に考え、得意な教科から指導することで自信を持ってもらうことを重視しています。
まずはその第一歩として、自宅でもオンラインでも受けられる無料体験授業を、ぜひお気軽にお試しください!