こんにちは、あすなろスタッフのカワイです。
多項式の計算という単元の解説をしていきます!
この単元では「文字が入った要素同士の計算」が出来るようになることが目標です。1年生の時に学習した「文字と式」が土台となるので、もし不安な人は復習してから読み進んでみて下さい!
この記事では、単項式・多項式の単元で登場する数学用語の解説をしていきます。といっても、基本的に中1の内容に少し新しい要素を加えるだけです!
最後に確認問題もあるので、良かったら最後まで読んでみて下さいね!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校2年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
単項式とは?
単項式とは、数字や文字についての乗法・除法だけでつくられた式のことをいいます。次のようなものです。
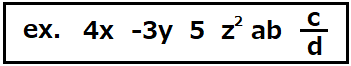
上にあるものの特徴を挙げてみると、
- 数字のみ
- 文字のみ
- 数字と文字がある
- +や-がない
などですね。かけ算やわり算は含まれていますが、足し算や引き算が無いものが単項式になります。
多項式とは?
単項式とは、1つの項の式を表すものでした。それに対して2つ以上の項の式を表すものを多項式といいます。例えば、次のようなものです。

特徴を挙げると
- 数字と文字が混在
- +や-がある
などがあります。
このように、+や-によって項が2つ以上連なった式を多項式と呼びます。
ところで、3+4のようなものは多項式とは呼ばれません。
なぜなら、3+4=7と計算することができ、単項式の形に出来てしまうからです。
また、a+3aなども同じようにa+3a=4aと計算できてしまうので多項式とは呼べません。
つまり、項が二つ以上あり、単項式の形に出来ないものが多項式といえます!
次数とは?
単項式と多項式がどのようなものなのかを説明しましたが、これらをさらに分類することができます。
何で分類するのかというと、掛けられている文字の数です!
掛けられている文字の数のことを次数(じすう)と呼びます。
単項式の次数の数え方
単項式の場合は、非常に簡単です。その式に入っている文字の数を数えてみましょう。
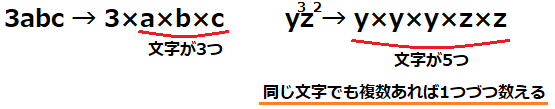
左の項の場合、a,b,cの3つがあるので文字数は3です。数字の3は文字ではないので、次数の計算にはカウントされません。
したがって、3abcの次数は3となります。
右の項の場合、yとzがそれぞれ乗数となっています。これらをバラバラにするとyが3つとzが2つの合計5つの文字があることが分かります。
したがって、\(y^3z^2\)の次数は5となります。
多項式の次数の数え方
多項式の場合は、2つ以上の項の文字数を数えることになりますが、各項での文字数の数え方は単項数と同じです!
全ての項について次数を数えたら、最後に一番文字数が多い項を探し、その項の文字数=次数となります。次の例で確認してみましょう。

左の例から見ていきます。
\(a^{3}+5a^{2}-3a-2\)は、各項が累乗となっていますね。これを分解してそれぞれ次数を見ていくと、項の次数はそれぞれ3,2,1,0となっていると分かります。
この中で最も項の次数が大きいのは\(a^{3}\)の3なので、多項式の次数は3となります!
\(ab^{3}-c^{2}d+e\)も同様に各項を分解していくと、各項の次数は4,3,1となっていることが分かります。この中で最も次数が大きいのは\(ab^{3}\)の4なので、この多項式の次数は4となります。
まとめ
文字や数字が入った項が1つの式 →単項式
文字や数字が入った項が2つ以上の式 →多項式
式中の最も文字が掛けられている項の文字数 →次数
理解度を確認したい人は、次の[やってみよう!]を解いてみて下さい!
やってみよう!
問題
次の式の次数を答えよう
- $$3def$$
- $$4a^{2}+3b+1$$
- $$6ab-\frac{c}{5}$$
答え
- \(3\)
- \(2\)
- \(2\)
\(def\)の3つの文字があるため、次数は3である。
一つ一つの項の次数を見ていくと、左から順に2,1,0となる。したがって、次数は2である。
一つ一つの項の次数を見ていくと、左から順に2,1となる。したがって、次数は2である。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。