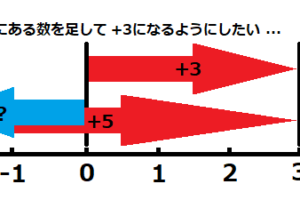
こんにちは、あすなろスタッフのカワイです。
今回から、比例と反比例という単元の解説を始めていきますが、実際にこれらの話をする前にまず、関数というものについて0から教えていきます。
比例・反比例を理解すると、今の数がどのように変化するのか、変化してきたのか、その一部を理解することができるようになります。
実際に勉強していく流れについては、意外とそこまで目新しい事はやりません。しかしながら、新しく出てくる数学用語もあるので、それらを少しずつ理解しつつ、まず関数から理解を深めていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
関数とは?
ここまで「関数」という言葉を出してきましたが、そもそも関数ってなんだ?と思ったと思います。ここで説明させてもらいますね。
関数とは、ある数を入れたときに、別の決まった数が1つに決まるもの、と考えてもらえばいいです。
下の図を見てください。

関数のイメージはこんな感じです。ある数(例ではA)を関数に入れると、別の決まった1つの数(例ではB)が出されます。これは、関数という箱の中で、Aという数がBという数に変換されたということになります。
これは、何回同じ動作を行っても、必ずBが出てくるということになります。
では、この関数に対して別の数「C」を入れてみましょう。

Cを入れてもBが出てくる、と思いきや、今度はDが出てきました。
「あれ、Bが出てくるんじゃないの?」と思った人、少し考えてみてください。

関数というのは、ある入る数が変わると、出てくる数も変わります。ある数に対して、値が決定するものを関数と呼ぶので、別の数を入れたら、当然Bではない別の数が返ってくるわけです。
ここで、今書いてきたAやBやCやDのことを「変数」と言います。
変数というのは、そこに任意の数を入れることができる数です。一次方程式で「\(x\)」や「\(y\)」などを用いて計算を進めてきたと思いますが、その文字のことです。
では、具体的に関数とはどのようなものが入るでしょうか。
少し見ていきましょう!
関数の中身とは…?
では仮に関数を\(y=3x\)としましょう。下の図を見てください!
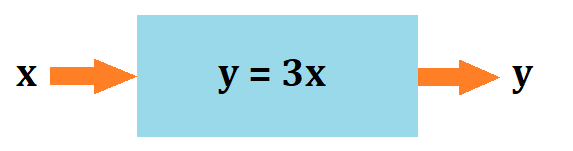
このような形になることがわかります。
この関数は、式からわかる通り、\(x\)にある数を入れると、その3倍の数を\(y\)として出す、という意味となっています。
したがって、\(x\)に適当な数字を入れてみると、
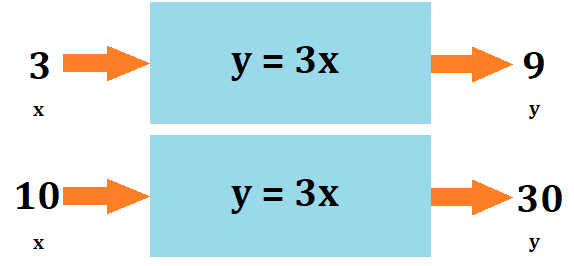
こうなります。
今回は\(x\)に\(3\)と\(10\)という数を入れてみましたが、出てくる値\(y\)は当然別で、それぞれ\(9\)と\(30\)となります。
このようなものが関数と覚えてもらえたら大丈夫です。
比例・反比例とはなんだ
ここまで関数、変数など一見関係なさそうな単語の解説ばかり聞かされてウンザリかもしれませんが、ここでやっと比例・反比例とは何か、簡単に解説します。
比例とは、入れる変数が2倍、3倍になると、それに準じて出てくる変数が2倍、3倍となる関係を言います。ちょっと説明がわかりずらくなってしまいました。
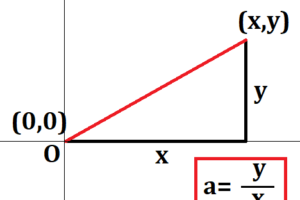
\(y=3x\)というさっきの式から引用すると、\(x\)と\(y\)は比例の関係ということができます。というのも、入れる変数の値を1増やしたら急に100増えたり、逆に数字が減ったりすることはありません。
ここで、この式でいう3の部分のことを「比例定数」と呼びます。下にわかりやすそうな図も入れておきますね。
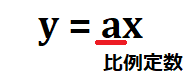
逆に、反比例というのは何かというと、入れる変数が2倍、3倍となると、出てくる変数が\(\frac{1}{2}\)倍、\(\frac{1}{3}\)倍となる関係のことをいいます。この時の式の一定の値となる部分も、同様に比例定数といいます。間違えやすいので注意してください!
これらの式については、次回から詳しく解説していくので、今回は意味だけでもしっかり理解してもらえたらOKです。
まとめ
いかがでしたでしょうか。関数についてや比例・反比例について理解してもらえたら幸いです。今回は語句の説明がメインになってしまいましたが、次回から比例ってなに?というところに入っていきます。新しい知識を得ることを楽しみながら、次回も頑張っていきましょう!