こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、2次方程式を解く最強の公式である、解の公式を解説していきます!
「既に学校で勉強したから、公式は何となく見たことがあるけど、どうしてこれで解けているのか分からない」という人が結構いると思います。
なので、今回のこの記事では、どのようにその公式が導き出されているかということについて、詳しく解説していきたいと思います。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
解の公式とは?
解の公式は、\(ax^{2}+bx+c=0\)(\(a≠0\))のとき、
$$\LARGE x=\frac{-b±\sqrt{b^{2}-4ac}}{2a}$$
となります。これはどのような公式かというと、
$$2x^{2}+5x+3=0$$
という二次方程式があったときに、
上の\(ax^{2}+bx+c=0\)と照らし合わせて、
\(a=2,b=5,c=3\)
とします。これを解の公式にそのまま入れ込むと、
$$x=\frac{-5±\sqrt{5^{2}-4×2×3}}{2×2}$$
$$x=\frac{-5±1}{4}$$
となり、
\(x=-1,x=-\frac{3}{2}\)
となります。
解の公式さえ覚えれば、公式に値を入れ込むだけで解く事が出来るので、非常に簡単な方法です。
この公式によって、何故解くことが出来るのかについて、公式を証明することによって解決していきましょう。
文字が多く出てきますが、1つ1つゆっくり理解しながら進めていってくださいね。
公式の証明(極力分かりやすく)

では、一般的な2次方程式として、\(ax^{2}+bx+c=0\)(\(a≠0\))の式から進めていきます。
ここで、\(a≠0\)としているのは、
\(a=0\)のとき、上の式は\(bx+c=0\)となり、これはもはや2次方程式ではないからです。また、\(a=0\)では、割り算が出来ません。
では話に戻りましょう。
\(\LARGE ax^{2}+bx+c=0\)
の両辺を\(a\)で割ってみます。すると、
\(\LARGE x^{2}+\frac{b}{a}x+\frac{c}{a}=0\)
となります。全ての項を\(a\)で割った形になっていますね。
\(ax^{2}\)の部分は\(a\)で割ると、ただの\(x^{2}\)になります。
平方完成で\(x\)の次数を減らす
次が重要です。
\(x^{2}+\frac{b}{a}x\)の部分について考えてみましょう。
\(x\)の次数が異なるものがあると、これを\(x\)の形にするのは難しいです。
そこで\((x+α)^{2}\)という2乗の形にすることによって、実質の次数を減らそうという算段です。(\(α\)は場合によって変わる値です)
上の\((x+α)^{2}\)を展開すると、\(x^2+2αx+α^2\)となります。
\(α\)の部分を今回解いている\(x^2+\frac{b}{a}x\)に当てはめてみると、\(2αx\)の部分が\(\frac{b}{a}x\)となれば、\((x+〇)\)の形にすることができそうです。
\(2αx=\frac{b}{a}x\)
より
\(α\)は\(\frac{b}{2a}\)となります。
従って、\((x+\frac{b}{2a})^{2}\)となるのですが、これでは不完全です。
なぜなら、これを展開すると、
\(x^{2}+\frac{b}{a}x+\frac{b^{2}}{4a^{2}}\)となりますが、
\(\frac{b^{2}}{4a^{2}}\)の部分が、元々の方程式になかった部分でした。
ただ、\((x+α)^{2}\)の形を作りたかったら、必ずついてきてしまいます。さて、どうしたらいいでしょうか。
答えは単純です。その値を打ち消せるような値を入れてあげればいいのです。
従って、\(x^{2}+\frac{b}{a}x+\frac{b^{2}}{4a^{2}}-\frac{b^{2}}{4a^{2}}\)
とすると、\((x+\frac{b}{2a})^{2}-\frac{b^{2}}{4a^{2}}\)となります。
これはあくまで、\(x^{2}+\frac{b}{a}x\)の部分のお話なので、方程式全体の式に戻してあげると、
\(\LARGE (x+\frac{b}{2a})^{2}-\frac{b^{2}}{4a^{2}}+\frac{c}{a}=0\)
となります。
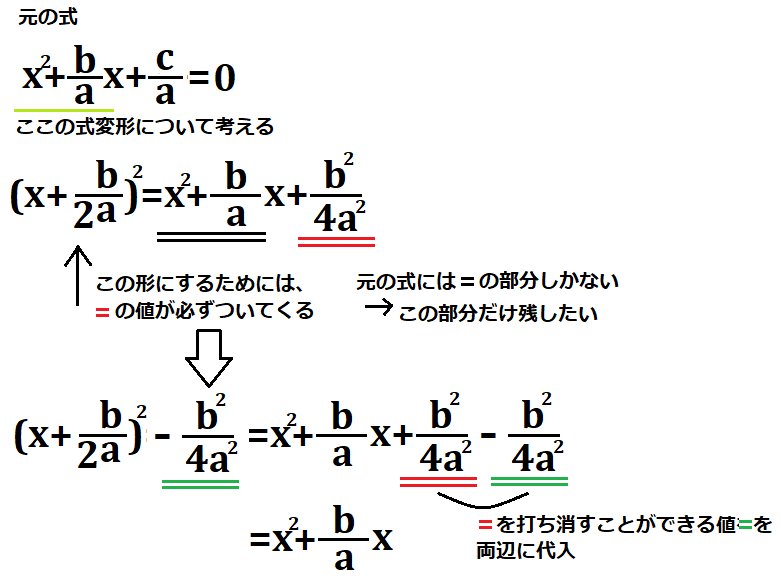
簡単にまとめると、上のようになります。
このような一連の処理を平方完成といいます。平方完成は非常に重要な式変形の手法なので、慣れていくのが重要です。
別記事でも紹介しているので、よろしければそちらを読んでみてください。
参考記事:【中3数学】平方完成を用いた2次方程式のやり方(解き方)について解説します!

さて、式展開の山場は超えました。
\((x+\frac{b}{2a})^{2}-\frac{b^{2}}{4a^{2}}+\frac{c}{a}=0\)
の変数を含まない項を右辺に移項すると、
\(\LARGE (x+\frac{b}{2a})^{2}=\frac{b^{2}}{4a^{2}}-\frac{c}{a}\)
とできますね。この右辺ですが、分母を\(4a^{2}\)に揃えて項をまとめると、
\(\LARGE (x+\frac{b}{2a})^{2}=\frac{b^{2}-4ac}{4a^{2}}\)
となります。
さて、この形に見覚えはありませんか?
これは、
\((x+α)^{2}=β\)
という式があった時に、
\(x+α=±\sqrt{β}\)
という形にすることが出来ます。
今の式の形を見てみると、これも両辺に平方根を取ることができるとわかります。従って、
\(\LARGE x+\frac{b}{2a}=±\sqrt{\frac{b^{2}-4ac}{4a^{2}}}\)
となります。
後は、左辺を\(x\)の形にするために、\(\frac{b}{2a}\)を右辺に移動すればいいので、
\(\LARGE x=-\frac{b}{2a} ±\sqrt{\frac{b^{2}-4ac}{4a^{2}}}\)
となり、\(x\)の形にすることができました!
最後に、一番最初に紹介した形にするためには、右辺の\(4a^{2}\)の部分をルートを外した形にして、右辺を1つの項にまとめてあげると、
$$\LARGE x=\frac{-b±\sqrt{b^{2}-4ac}}{2a}$$
という式の完成です。
このように、解の公式というのは、
\(ax^{2}+bx+c=0\)という式変形からできています。この式の形は2次方程式を殆ど表すことができるので、この式一つで2次方程式の解を知ることが出来るのです。
まとめ
今回は、2次方程式の解の公式の導き方について紹介しました。
他の解き方もありますが、すべての問題に対して手早く解く方法はこれだけです。
極端に言えば、この解の公式を覚えさえすれば、2次方程式の解を確実に解くことが出来ます!
※個人的には、解の公式を覚えるよりも、解の公式の導き方を理解する方に時間を使うことをお勧めします!何故なら、解の公式自体をふと忘れてしまったときに、解の公式を自分で作ることが出来るからです!
今回解説した式変形を、何も見ずに何回か解くことが出来れば、すんなり覚えられます。
”ホントかな…?”と疑う考えがもしあるようでしたら、是非やってみてください!
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。