こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、平面図形である「円」を拡張した立体図形である「円柱」「円錐」「球」について、解説していきたいと思います。
基本的な考え方は角柱や角錐と同じですから、これらを勉強している人なら大丈夫だと思います。(角柱や角錐について学びたい方はこちら)
では、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校2年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
円柱
まず、円から平面から真っ直ぐ伸ばして(厚みを増やして)できる図形を作ってみようと思います。
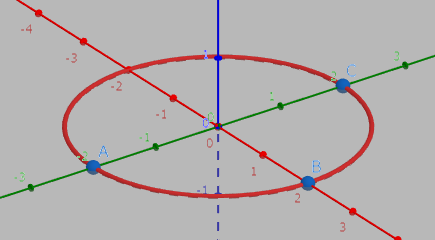
があったときに、これを高さ方向に伸ばしていくと、
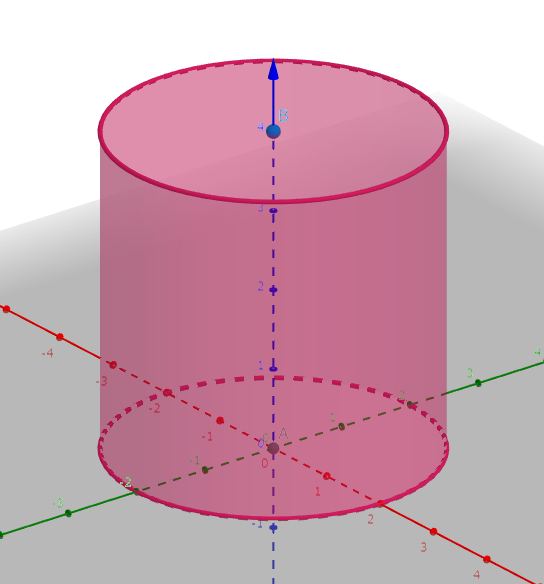
のようになります。これを円柱といいます。
さて、円柱はどのような要素から出来ているのか考えてみましょう。
まず、円柱には上下に円がありますね。これらは底面といいます。
つぎに、この円を取り囲むような図形がついていますね。
これらは平面図形で表すことが出来ませんが、角柱や角錐のときと同じように側面といいます。
ところで、円柱は、円周や側面の長さは変えられるものの、角柱のように他の形の底面が来ることがありません。
円柱は円だけが底面となる図形である、ということです。
また、明確に辺と呼べる場所がないことも大きな特徴です。その代わりに、母線という言い方をします。
母線はどこか特定の位置の線というよりかは、パッと見た時に、端となっている側面の部分の事です。
なぜそんな曖昧な言い方となるのかというと、円柱を底面の位置を変えずに、360°どこから見ても見え方は全く変わらないからです。正面が決まっていないのです。
その代わり、どこから見てその長さを取っても等しくなるので、辺のように扱っても問題がないということになります。
円錐
次に、角錐と同様に、ある一点に向かって伸ばしていったときの立体図形を考えてみましょう。

円柱と同じように、円を用意して、この上部に適当な点の位置を決めて、伸ばしていきます。
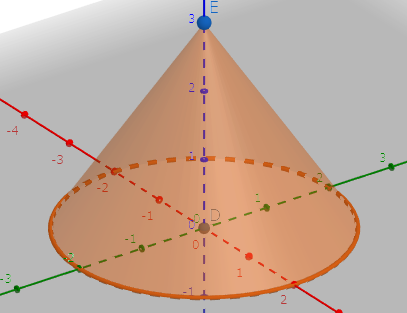
すると、上のようになります。これを円錐といいます。
角錐と同じように、底面が1つあり、後はクラッカーやアイスクリームのコーンのような部分でできています。このとがった部分を頂点といいます。
そして、円柱と同様に平面図形で表すことができない側面があり、その端の部分を母線といいます。
多角形と円による立体図形を比べてみる
さて、ここまで円柱と円錐について見てきましたが、これらは角柱や角錐とどう違うのか、改めてまとめてみます。
円柱と角柱を比べてみる
円柱と角柱を比べると、共通点と相違点があることに気付けると思います。
まず同じ点は、
- 底面が2つ
- 底面に対して真っ直ぐ側面が伸びていること
異なる点は、
- 底面の形
- 側面が平面図形で表せる(角柱)と表せない(円柱)
- 点や辺がある(角柱)と母線がある(円柱)
となります。
「○柱」という名前の立体図形は「底面が2つ」で「底面から上に真っ直ぐ側面がある」という点が共通しているということがこれで確認できましたね。
※底面から上に真っ直ぐ、という表現は、今後の勉強でいう垂直の事です。もしすでに習っている人がいたら、読み替えて下さい。
円錐と角錐を比べてみる
次に、円錐と角錐を比べてみます。
この2つが同じ点は、
- 底面が1つ
- 底面から頂点に対して側面が伸びていること
異なる点は、
- 底面の形
- 側面が平面図形で表せる(角柱)と表せない(円柱)
- 辺がある(角柱)と母線がある(円柱)
となります。
「○錐」という名前の立体図形は「底面が1つ」で「底面から頂点に対して伸びている」という点が共通しているということがこれで確認できます。
球
最後に、球についてお話ししようと思います。
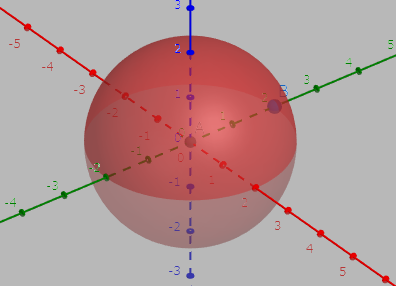
球はどこから見ても円に見える立体図形の事です。
円の特徴として辺や点が無い、という部分は同じで、球にも辺や点がありません。
球について詳しく触れるととても難しく面白いですが、とてもここで解説できる内容ではないので、興味がある方は調べてみて下さい!
まとめ
今回は円柱と円錐についてまとめました。○柱や○錐の特徴はそのままで、底面が円になることで変わる部分がいくつかあったと思います。
とにかく、今回は母線などの円からできる立体図形の性質を覚えたらOKです。
今後は、これらの立体図形の特徴を幾何学(きかがく)的に解けるようにする為に、平面や線の位置関係にについて勉強していきます。良かったら読んでみて下さいね!
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。