【中3数学】y=ax^2の値の変化が分からない方必見！グラフを使って解説します！

こんにちは、あすなろスタッフのカワイです！

今回は、\(y=ax^{2}\)のグラフから読み取れる事の1つである、値の変化について一つ一つ解説していきます！

やること自体は一次関数の時と変わりませんが、この\(y=ax^{2}\)という関数は\(x\)に対して一定に増えるわけではないので、少し頭を柔らかしておきましょう。

(「そもそも\(y=ax^{2}\)ってなに？」「\(y=ax^{2}\)のグラフを見たことが無い！」という人でも読み進められるように、簡潔な説明や関連ページの紹介もしているので、良かったらそのまま読み進んでみてくださいね！)

あすなろには、毎日たくさんのお悩みやご質問が寄せられます。

この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。

参照元：文部科学省　学習指導要領「生きる力」

【復習】\(y=ax^{2}\)とは？

\(y=ax^{2}\)とは、\(y\)が\(x\)の2乗に比例する関数です。

今まで勉強してきた\(y=ax\)では、\(x\)の値が1つ増えた時の\(y\)の増える量は一定でしたが、\(y=ax^{2}\)という式になると、\(x\)がどの値の時に1増えるかによって、\(y\)の増える量が変わるという特徴があります。

例えば、斜面を転がるボールの位置・時間を推測することが出来たりします。他にも様々な所で使われている関数です。

詳しくは→【中3数学】y=ax^2ってなに？y=ax^2が使われている例を解説します！

【復習】\(y=ax^{2}\)のグラフってどんな形をしているの？

\(y=ax^{2}\)のグラフは一次関数のような線形ではなく、放物線とよばれる曲線を描きます。

また、グラフの概形の最も下の部分もしくは最も上の部分が原点(\(x,y\))=(\(0,0\))を通り、いずれの場合も頂点といいます。

下のグラフが\(y=3x^{2}\)です。

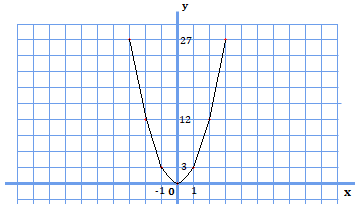
一方、下のグラフが\(y=-3x^{2}\)です。

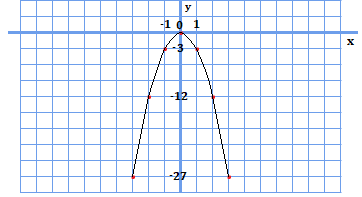
このように、係数\(a\)が正のときは上が開いた形に、負のときは下が開いた形となります。

より詳しく知りたい方は→【中3数学】y=ax^2のグラフってどんな形になるの？いくつかの特徴について解説！

\(y=ax^{2}\)グラフから値の変化を読み取ってみよう

\(y=ax^{2}\)のグラフがどのような形になっているのかが分かったところで、次にその値の変化について着目して考えてみたいと思います。

一次関数の場合は…？

そもそも、一次関数はどうだったかというと…

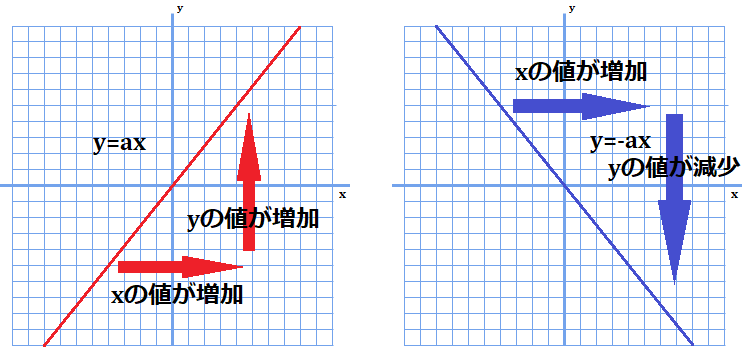
こんなグラフでした。一次関数の場合、\(x\)の値が増加すると、

• 係数\(a\)が正のときは常に増加する
• 係数\(a\)が負のときは常に減少する

という特徴があることが見て取れます。

\(y=ax^{2}\)の場合は…？

さて、\(y=ax^{2}\)のグラフはどんな概形かというと、

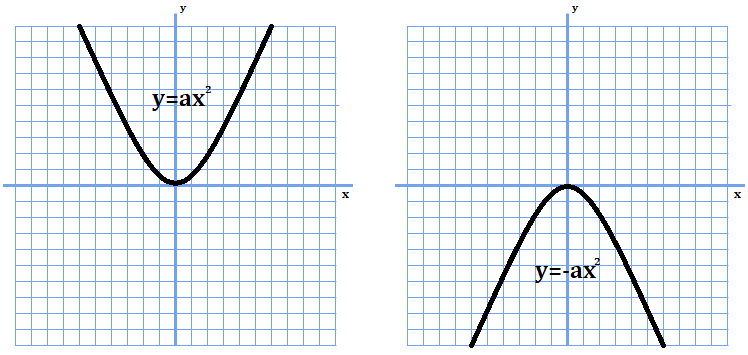
このような形でした。赤い点から\(x\)が増加する方向に考えてみましょう。

まず、\(x\)が負のときの\(y\)の値の増減を見てみます。

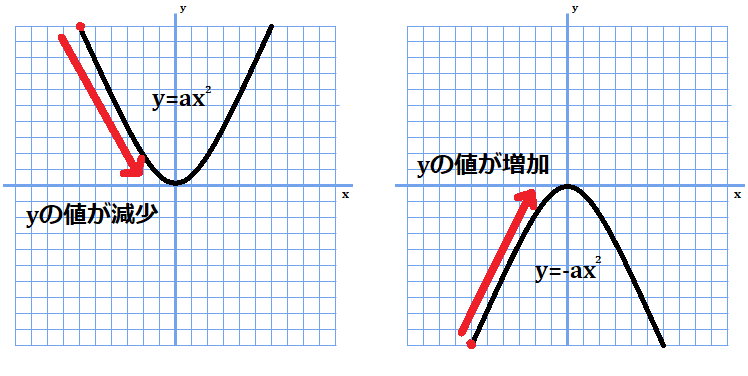
係数が正の場合、\(x\)が負の範囲にいるときは、\(x\)が増加すると\(y\)の値は減少する方向に進みます。

グラフの線が下向きに進んでいくのを見れば分かりますね。

一方、係数が負の場合、\(x\)の負の範囲にいるときは、\(x\)が増加すると\(y\)も増加する方向に進みます。

次に、\(x=0\)から増加した時の\(y\)の値の増減を見てみましょう。

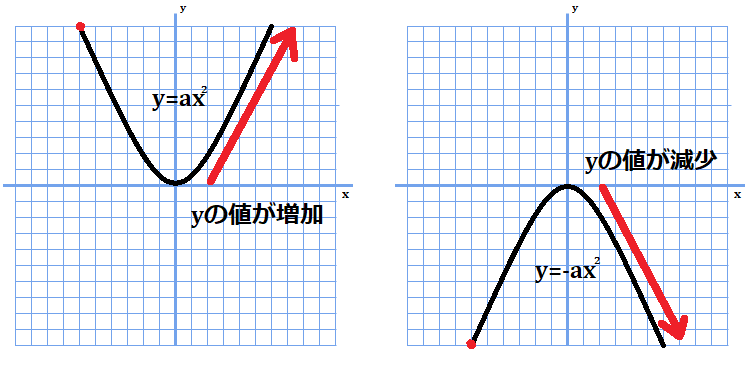
係数が正の場合、\(x\)が正の範囲にいるときは、\(x\)が増加すると、\(y\)の値も増加する方向に進みます。

係数が負の場合、\(x\)が増加すると、\(y\)が減少する方向に進みます。

このように、\(x\)の値が\(x=0\)すなわち原点に達した時、\(y\)が増えるか減るかが変わります。

このように、文章で書くと小難しく聞こえると思いますが、グラフの形と矢印の向きに着目して考えることで簡単に考えらえると思います！

まとめ

• \(y=ax^{2}\)(\(a＞0\))のとき
  • \(x\)が負の範囲にいるときは、\(x\)が増えると\(y\)が減る
  • \(x\)が正の範囲にいるときは、\(x\)が増えると\(y\)が増える
• \(y=ax^{2}\)(\(a＜0\))のとき
  • \(x\)が負の範囲にいるときは、\(x\)が増えると\(y\)が増える
  • \(x\)が正の範囲にいるときは、\(x\)が増えると\(y\)が減る

最後までご覧いただきありがとうございました。

｢数学でわからないところがある｣そんな時に役立つのが、勉強お役立ち情報！

数学の単元のポイントや勉強のコツをご紹介しています。

ぜひ参考にして、テストの点数アップに役立ててみてくださいね。

もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。