こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、\(y=ax^{2}\)という式がどのようなグラフとなるのか、またグラフからどのようなことが読み取れるかについて解説していきたいと思います!
「そもそも、\(y=ax^{2}\)って何…?」という方もいると思いますので、そういった方でも読み進められるようにしていますので、良かったら最後まで読んでみてもらえたらと思います!
では、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。
参照元:文部科学省 学習指導要領「生きる力」
=もくじ=
【復習】\(y=ax^{2}\)とは?
\(y=ax^{2}\)とは、\(y\)が\(x\)の2乗に比例する関数です。
今まで勉強してきた\(y=ax\)では、\(x\)の値が1つ増えた時の\(y\)の増える量は一定でしたが、\(y=ax^{2}\)という式になると、\(x\)がどの値の時に1増えるかによって、\(y\)の増える量が変わるという特徴があります。
例えば、斜面を転がるボールの位置・時間を推測することが出来たりします。他にも様々な所で使われている関数です。
詳しくは→【中3数学】y=ax^2ってなに?y=ax^2が使われている例を解説します!
\(y=x^{2}\)のグラフ
\(y=x^{2}\)は、\(y\)が\(x\)の2乗に比例するグラフの中でも最も単純な式ですね。ですから、まずこの\(y=x^{2}\)という式のグラフの形から考えていこうと思います。
まず、\(x\)が\(3\)〜\(-3\)の範囲で考えてみましょう。これを\(1\)ずつ変えて\(y=x^{2}\)の式に代入すると、
| \(x\) | \(-3\) | \(-2\) | \(-1\) | \(0\) | \(1\) | \(2\) | \(3\) |
| \(y\) | \(9\) | \(4\) | \(1\) | \(0\) | \(1\) | \(4\) | \(9\) |
となります。
ただ点をつなぐだけでは歪な形のグラフになる
さて、これをグラフに落とし込むとどのようになるか考えてみると、
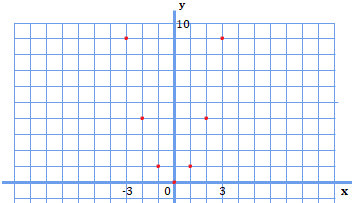
上のようになります。線をつないでみると、
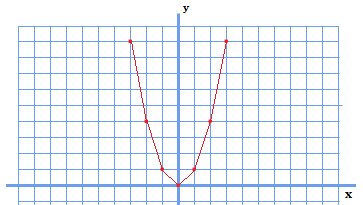
このような形が見えてきます。\(x\)が\(-1\)→\(1\)になるあたりまでは形が角ばっているようで、そこから先は滑らかに上がっていくといった関数となっています。
また、表からもわかったことではありますが、原点を通り、\(x=0\)を中心として鏡写しになったように点が来ていることが分かります。
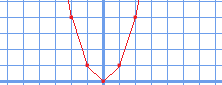
しかし、\(x\)の値が1変わるだけで、グラフの進行方向がこのような急激な変化になるとは考えにくいのです。\(x\)の値が大きくなるにつれて変化量が変わってくるならば、0や1の間の、例えば0→0.5なんかは0→1よりも緩やかな増加でなくてはおかしいと思うのです。
実際、このように少しの点だけを適当な線を繋いだグラフというのは、比例グラフとは違い、正確ではないです!
もう少し細かく値をとってみよう
上の反省を生かして、今度は\(x\)が\(-1\)から\(1\)の範囲で\(-1\)ごとに細かく取っていこうと思います。すると、
| \(x\) | \(-1\) | \(-0.9\) | \(-0.8\) | \(-0.7\) | \(-0.6\) | \(-0.5\) | \(-0.4\) | \(-0.3\) | \(-0.2\) | \(-0.1\) |
| \(y\) | \(1\) | \(0.81\) | \(0.64\) | \(0.49\) | \(0.36\) | \(0.25\) | \(0.16\) | \(0.09\) | \(0.04\) | \(0.01\) |
| \(0\) | \(0.1\) | \(0.2\) | \(0.3\) | \(0.4\) | \(0.5\) | \(0.6\) | \(0.7\) | \(0.8\) | \(0.9\) | \(1\) |
| \(0\) | \(0.01\) | \(0.04\) | \(0.09\) | \(0.16\) | \(0.25\) | \(0.36\) | \(0.49\) | \(0.64\) | \(0.81\) | \(1\) |
このような形で値が取れました。細かいですが、これをグラフに適用してみると、
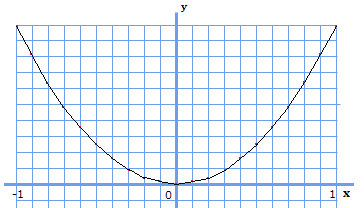
\(-1\)→\(1\)の範囲であっても非常に滑らかな図がかけました。どの細かい範囲で値をとっても、常にその変化量が変わっている、ということが分かってもらえたらと思います。
ここまででまず分かったことは、
- ボールを投げた時の軌道の逆のような形をしている
- 原点を通る
- \(y\)軸を対称軸として左右対称である
ですね。
1番目に述べた「ボールを投げた…」のような形状のグラフのことを放物線といい、\(y=x^{2}\)の値はまさしく放物線を書いたような分布になります。なので、ただ単に直線を描くようなグラフの書き方では上手く示すことが出来なかった、ということなのです。
また、2番目と3番目の原点となっている部分の事を頂点といいます。
\(y=3x^{2}\)のグラフ
では次に、\(y=3x^{2}\)のグラフについても考えてみましょう。
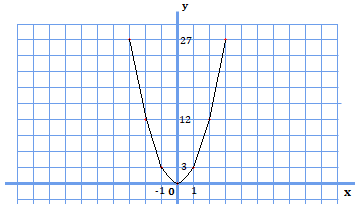
\(y=x^{2}\)と比較すると、増えていく値の変化量が変わるだけであり、形状は放物線と、さっきのグラフと同じようになっています。
\(y=x^{2}\)のグラフとの比較
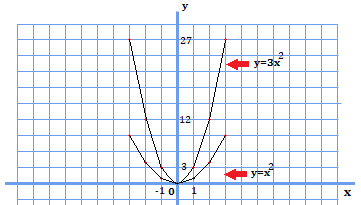
次に、\(y=x^{2}\)と\(y=3x^{2}\)の比較をしてみます。\(y=ax^{2}\)でいうところの\(a\)(係数)が大きい方が、グラフの傾きが急になっています。
\(y=-3x^{2}\)のグラフ
比例のグラフでもそうでしたが、変数(今回の場合は\(x\))の係数(\(a\))が大きくなるほど、グラフの傾きは大きくなります。
最後に、係数がマイナスである\(y=-3x^{2}\)について考えてみましょう。
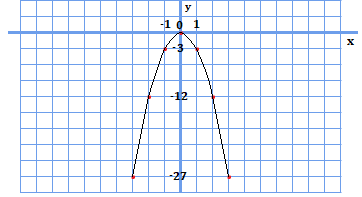
このグラフは、上に挙げた2つとは異なる点がありますね。上に挙げた2つの形は上に開いた形をしていますが、今回のグラフは放物線という文字通り、物を放ったような下に開いた形をしています。
\(y=3x^{2}\)のグラフとの比較
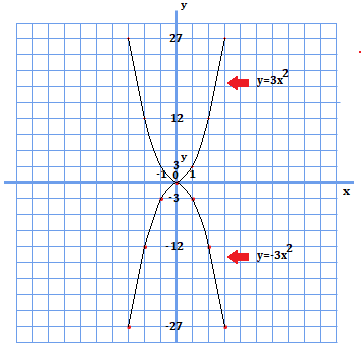
さて、係数の絶対値は等しく、符号が異なる「\(y=3x^{2}\)」と比較してみます。すると、\(x\)軸を対称軸として反転したような形になりました。
ということは、符号が変わっても、係数が同じであれば、そのグラフの傾きの大きさ自体は変わらないということです。
まとめ
\(y=ax^{2}\)の特徴
- 原点を通る
- \(y\)軸について対称であり、その概形は放物線となる。
- 係数\(a\)が大きな値であるほど、その傾きは急になる。
- 係数\(a\)が正の場合は、上が開いた形になり、 係数\(a\)が負の場合は、下が開いた形となる。
いかがでしたでしょうか。今までと見慣れない形のグラフだったと思いますが、係数の大きさによってグラフの傾きが大きくなるなど、今まで学んできた内容の知識から納得できる部分もあったと思います。
グラフは表を作って、その表を元に座標にプロットしていけば描けるので、様々な\(y=ax^{2}\)グラフを描いてみてはいかがでしょうか。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。