こんにちは、家庭教師のあすなろスタッフのカワイです。
今回のページでは、\(y=ax^{2}\)という関数の変化の割合について考えていきたいと思います。
\(y=ax^{2}\)の前に一次関数の例から考えていくので、「そもそも変化の割合ってなんだっけ？」となっている人でも理解できると思います！
また、\(y=ax^{2}\)についてや\(y=ax^{2}\)のグラフについて不安な方でも理解できるように、簡単な解説や詳しい解説ページへのリンクも紹介しています！是非読み進めてみて下さい。
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。
参照元：文部科学省 学習指導要領「生きる力」
=もくじ=
【復習】\(y=ax^{2}\)とは？
\(y=ax^{2}\)とは、\(y\)が\(x\)の2乗に比例する関数です。
今まで勉強してきた\(y=ax\)では、\(x\)の値が1つ増えた時の\(y\)の増える量は一定でしたが、\(y=ax^{2}\)という式になると、\(x\)がどの値の時に1増えるかによって、\(y\)の増える量が変わるという特徴があります。
例えば、斜面を転がるボールの位置・時間を推測することが出来たりします。他にも様々な所で使われている関数です。
詳しくは→【中3数学】y=ax^2ってなに？y=ax^2が使われている例を解説します！
【復習】\(y=ax^{2}\)のグラフってどんな形をしているの？
\(y=ax^{2}\)のグラフは一次関数のような線形ではなく、放物線とよばれる曲線を描きます。
また、グラフの概形の最も下の部分もしくは最も上の部分が原点(\(x,y\))=(\(0,0\))を通り、いずれの場合も頂点といいます。
下のグラフが\(y=3x^{2}\)です。
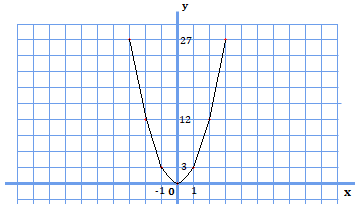
一方、下のグラフが\(y=-3x^{2}\)です。
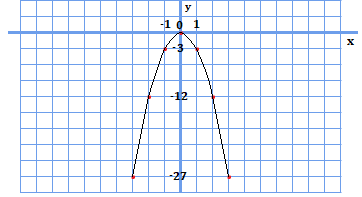
このように、係数\(a\)が正のときは上が開いた形に、負のときは下が開いた形となります。
より詳しく知りたい方は→【中3数学】y=ax^2のグラフってどんな形になるの？いくつかの特徴について解説！
変化の割合とは？
では、先に「変化の割合」とはなにか復習しておきましょう。
変化の割合とは、「ある関数で\(x\)が増加し、\(y\)が増加した時に、\(y\)の増加量を\(x\)の増加量で割ったもの」となります。式で表すと、
$$y=\frac{yの増加量}{xの増加量}$$
となります。変域とは違い、\(x\)がAからBまでと指定されたら、そのAとBのときの\(y\)の値さえわかれば、変化の割合を求めることが出来ます。なので、基本的に代入すれば求める事が出来るということですね。
例えば、\(x\)が\(1\)から\(2\)まで移動したときに、\(y\)が\(2\)から\(4\)まで変化する場合、
$$変化の割合=\frac{4-2}{2-1}$$
と表され、計算すると\(2\)となります。
しかし、代入するだけではただの作業となってしまい身につかないので、今回は一次関数の場合と比較して、その意味を考えていきましょう。
一次関数の時は？
\(y=3x-2\)という関数を例に考えてみましょう。
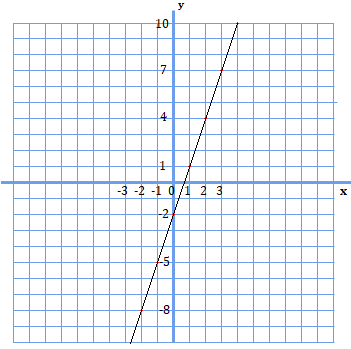
例えば、\(x\)が\(1\)から\(3\)まで増加する時の変化の割合を考えるとすると、
\(y=3x-2\)に\(x=1\)を代入して、\(y=1\)
\(y=3x-2\)に\(x=3\)を代入して、\(y=7\)
となるので、変化の割合は、
\(\frac{7-1}{3-1}=\frac{6}{2}=3\)
となり、\(3\)が変化の割合となります。
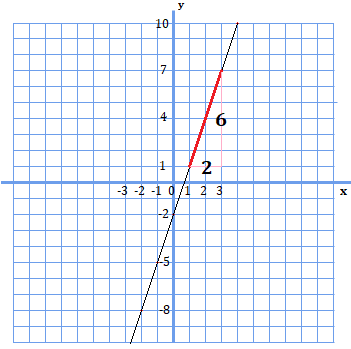
では、\(x\)が\(-2\)から\(1\)まで移動するときはどうかというと、
変化の割合\(=\frac{1-(-8)}{1-(-2)}=\frac{9}{3}=3\)
となり、\(3\)です。
どこからどこまで指定しても、変化量は\(3\)でずっと変わりません。
何故かというと、この\(3\)は\(y=3x-2\)の\(3\)の部分と一致していて、変化の割合はグラフの傾きと完全に一致します。
変化の割合は直線で表されるということを知った上で、\(y=ax^{2}\)のグラフについて考えてみましょう。
\(y=ax^{2}\)の変化の割合について考えよう\)
例1.\(y=x^{2}\)について、\(x\)が\(1\)から\(3\)まで増加する時の変化の割合を求めよう。
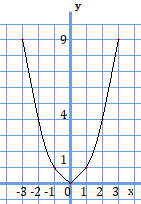
一次関数と同じように、\(x\)に\(1\)と\(3\)を代入して変化量を調べてみます。
\(y=x^{2}\)に\(x=1\)を代入して、\(y=1\)
\(y=x^{2}\)に\(x=3\)を代入して、\(y=9\)
となるので、変化の割合は、
\(\frac{9-1}{3-1}=\frac{8}{2}=4\)
となり、\(4\)が変化の割合となります。
これをグラフ上で示してみると、
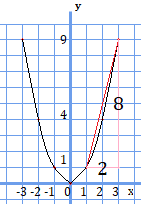
となります。赤で示したものが、変化の割合を示す線です。グラフは曲線なのに対し、変化の割合は直線であらわされます。
例2.\(y=x^{2}\)について、\(x\)が\(-3\)から\(2\)まで増加する時の変化の割合を求めよう。
さて、今度はこれを\(-3\)から\(2\)まで移動させるとどうなるのか考えてみようと思います。
\(y=x^{2}\)に\(x=-3\)を代入して、\(y=9\)
\(y=x^{2}\)に\(x=2\)を代入して、\(y=4\)
となるので、変化の割合は、
\(\frac{4-9}{2-(-3)}=\frac{-5}{5}=-1\)
となり、\(-1\)が変化の割合となります。
同じ関数上の変化の割合を出したのですが、\(1→3\)では\(4\)なのに対し、\(-3→2\)では\(-1\)となっています。
グラフ上に示してみると、
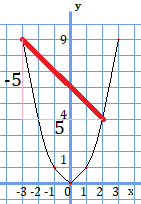
となります。
どこからどこまでを計るかによって、変化の割合は変わってきます。赤線の傾きを調べることで、変化の割合が分かります。
例3.\(y=-x^{2}\)について、\(x\)が\(-1\)から\(2\)まで増加するときの変化の割合を求めよう。
最後に、\(y=-x^{2}\)について考えてみましょう。考え方は同じです。
\(y=-x^{2}\)に\(x=-1\)を代入して、\(y=-1\)
\(y=-x^{2}\)に\(x=2\)を代入して、\(y=-4\)
となるので、変化の割合は、
\(\frac{-4-(-1)}{2-(-1)}=\frac{-5}{5}=-1\)
となり、\(-1\)が変化の割合となります。
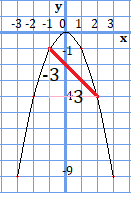
グラフにすると、上の感じです。
変化の割合は式によって求められますが、今までやってきたようにグラフを使って調べると、視覚的に分かるので、見直しをする際にいいと思います。
【応用】\(y=ax^{2}\)の変化の割合をより早く解く方法！
実は、この変化の割合をより早く解く方法があるのです。
\(y=ax^{2}\)について、\(x\)が\(α\)から\(β\)まで変化するときの変化の割合は、
$$「変化の割合」=a(α+β)$$
で求めることが出来ます。ただの足し算をするだけで終了です。
公式
何故これで求められるかを説明します。変化の割合を考えた時に、
\(「変化の割合」=\frac{「yの変化量」}{「xの変化量」}=\frac{aβ^{2}-aα^{2}}{β-α}\)
と式変形することが出来ます。「\(y\)の変化量」というのは、すなわち、「変化後の\(y\)から変化前の\(y\)を引けばいい」ので、
変化後の\(x\)の値(\(β\))を代入した値「\(aβ^{2}\)」-変化前の\(x\)の値(\(α\))を代入した値「\(aα^{2}\)」となればいいということになります。これが上の式の分子部分の意味です。
さて、2乗-2乗の形は因数分解が出来るので、
\(=\frac{a(β-α)(β+α)}{β-α}\)
と分解することが出来ます。すると分子と分母に同じ部分が出来るので、これを打ち消しあうと、最初に説明した\(a(α+β)\)となります。
簡単に解ける公式を用いた例
さて、この式を用いて先程解説した「例3.\(y=-x^{2}\)について、\(x\)が\(-1\)から\(2\)まで増加するときの変化の割合を求めよう。」を解いてみましょう。
\(y=-x^{2}\)の比例定数は\(-1\)であり、変化は上の通りなので、これを代入すると、
\(a(α+β)=(-1)((-1)+2)=(-1)×1=-1\)
となります。
当然ながら、例3で導いた答えと一致していますね。
簡単な公式を用いる際の注意
この公式は、本当に手軽に変化の割合を導くことが出来るので、非常に便利です。
しかし、簡単に解けるようになってしまう式ほど注意した方がいいです。私が思う注意点は、
- 基本的な考え方が分かっている
- なぜこれで解けるのか理解している
の2点です。基本的な考え方が分かっていない人が使ってしまうと、少しひねった問題が出た際に対応できなくなってしまいます。基本に立ち返っても解けることが前提で、高速に求める為に使うようにしましょう！
まとめ
- 一次関数の変化の割合は、比例係数に等しい。
- \(y=ax^{2}\)の変化の割合は、比例係数によらず、「○から△まで」により決まる。
やってみよう！
次の変化の割合を求めよう。
- \(y=x^{2}\)について、\(x\)の値が\(-3\)から\(2\)までの変化の割合
- \(y=3x^{2}\)について、\(x\)の値が\(-2\)から\(1\)までの変化の割合
- \(y=-2x^{2}\)について、\(x\)の値が\(-1\)から\(3\)までの変化の割合
- \(y=-x^{2}\)について、\(x\)の値が\(-2\)から\(2\)までの変化の割合
こたえ
- \(-1\)
- \(-3\)
- \(-4\)
- \(0\)
最後までご覧いただきありがとうございました。
｢数学でわからないところがある｣そんな時に役立つのが、勉強お役立ち情報！
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。
