こんにちは、あすなろスタッフのカワイです。
今回は「文字と式」という単元の一番最初の内容になります!文字の式の中での用い方・ルールについて今回お話していこうと思います。
そもそも、式に文字を入れるということに違和感を持つ人もいるのではないでしょうか?見た目が数字ではないのですから無理はないですね。
ですが、中学数学では文字が入ることが当たり前になります!
そして、この文字というのが中々に便利なものなので、この良さが分かれば違和感なく受け入れることができるようになると思います!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
長方形の公式を文字で表す!
はじめに、例として長方形の面積を文字式で表してみましょう。

問題です。横の長さが4で縦の長さが3のとき、面積はいくつになるでしょうか?
求める為の式は
4×3
と表せるので、答えは
12
となりますね。
では、もし横の長さが5で縦の長さが8だったら、面積はいくつでしょうか?
求める為の式は
5×8
となり、答えは
40
となります。私たちは、これらを求めるときに、どのように考えて上のような式として表しているのでしょうか?
おそらく、「横の長さ」×「縦の長さ」(縦の長さ×横の長さ)と考えたと思います。
なぜこれが出てくるかというと、この「横の長さ」と「縦の長さ」にどんな数(正の数)を入れても、答えが出てくると知っているからです。
こういったものを小学校で「公式」といって学んだと思いますが、これは文字を使って式に書き換えることができます!
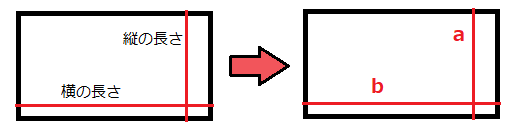
横の長さをa、縦の長さをbと置くことにします。すると、式は
a×b
となります!さっきまでの「横の長さ」×「縦の長さ」と同じことを式として表しています。

長方形の公式と同様に、aやbに好きな数(正の数)を入れたら、何らかの面積が出せます。
このように、文字は「中に色々な数字を入れられる万能なもの」と思ってもらえれば結構です!
文字を使えば、具体的な数字が分かっていなかったり、数字が変化したりする場合に柔軟に表現できます。
三角形の公式を文字で表す!
同様に、三角形の面積を文字で表してみましょう。
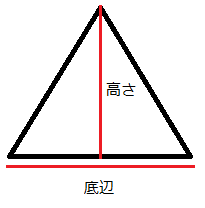
三角形の公式は長方形と違って、
底辺×高さ÷2
で求められるのでしたね。
今度は底辺をc、高さをdと置いてみます。
式に表すと
c×d÷2
となります。長方形と同様、文字で表すことができました!実際に文字のところに数字を入れてもらうと、これらの文字もどんな数(正の数)となっても成り立つことがわかると思います。

このように、今まで言葉で表していた公式などは、上で説明したように文字を含んだ式で表すことができます。
簡単な式を文字に置き換える!
小学校で習ったような公式以外の事柄も文字を含んだ式で示すことが可能です。
では、簡単な例を挙げてみましょう。
とある文房具屋で1つ100円のペンが売られていたとします。これを1本買うとき、式でどのように表しますか?きっと
100×1
と式で表すと思います。では2本買うときは?3本買うときは?…はたまた50本買うときは、どのように式で書くでしょうか?
難しく考える必要はありません。1本買うときと同じように書けば良いのです。
100×2
100×3
…
100×50
これらの式に共通点が見えてきませんか?
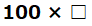
どれも、式はこのような形になっています。
この□に「買う本数」を入れたら、その本数買うときの代金の式になりますね。では、□すなわち「買う本数」をeという文字に置き換えてみましょう。式は下のようになります。
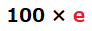
このeにはどんな自然数が入っても成り立ちます。
このように、1,2,3のような数字をなんでも入る文字に置き換えることができるようにしたものが、文字式となります。
まとめ
いかがでしたか?文字を式に入れていく過程を説明しましたが、あくまで文字は小学校の頃の□のようなもので「数字」が入れられる場所となります。ですから、文字はなんでも良いです。(昔からの流れでよく使われている文字などは多くありますが、本質的には文字は何でも構わないのです。)
難しく考えすぎず、□をかっこよく表現したバージョンなのだと理解して、使いこなしましょう!
やってみよう!
問題
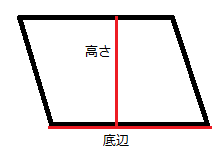
- 平行四辺形の面積の公式を文字で表そう。ヒント:高さをa,底辺をbとおいてみよう。
- ケーキを5人分買いたい。ケーキをx円とするとき、いくら必要でしょうか。求める式をつくってみよう。
答え
- 平行四辺形の面積は高さ×底辺(底辺×高さでもよい)で求められる。高さをa,底辺をbとおくと、 式はa×b(b×aでもよい)となる。
- かかるお金は「人数」×「ケーキの値段」で決まる。人数は5とわかっていて、ケーキの値段がx円なので、式は3×x となる。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。