こんにちは、あすなろスタッフのカワイです。
中学2年生の数学で「多項式」について学習したと思いますが、中学3年生では様々な多項式同士の計算もスムーズに解くことが出来るように解説していきます。
今回は、まず多項式について復習しながら、「単項式」と「多項式」の乗算について学習し、多項式同士の計算へ拡張していきましょう!
関連記事:【中2数学】単項式ってなに?多項式ってなんだろう?
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校2年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
復習:単項式、多項式とは?
単項式とは、\(+\)や\(-\)などの計算符号を含まない、それ自体を1つの数字としてみなすことが出来る項のことをいいます。
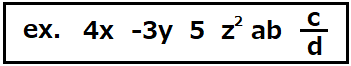
上に例を挙げてみました。\(-3y\)には-が含まれていますが、これはあくまで\(-1×3×y\)というものであるので、単項式です。
多項式とは、\(+\)や\(-\)などの計算符号を含んだ、複数の項で表された式のことをいいます。

上に多項式の例を挙げてみました。多項式は「単項式同士を足したり引いたりしたもの」という認識でも間違いありません。例えば、\(5x^{2}+4x-3\)の場合、\(5x^{2}\)と\(4x\)と\(-3\)という3つの単項式を足し合わせたものということができます。
単項式と多項式の乗法
単項式と多項式の違いを踏まえて、まずは単項式と多項式の乗法についてのいくつかの例を見ていきましょう。
例.\(2x(4y+3)\)
2年生の時は「数字」と「多項式」の計算を学習しましたが、数字が単項式に変わっただけで、計算の仕方は全く変わりません。分配法則を用いて計算していきます。
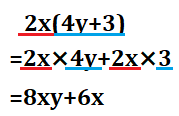
赤い下線の部分が単項式、水色の下線の部分が多項式とすると、多項式の部分を単項式に分解して、「単項式×単項式」の形にして計算します。それらを計算した結果、\(8xy+6x\)となりました。
「数字」×「多項式」であっても、「単項式」×「多項式」であっても、計算結果は「多項式」になります。
多項式と多項式の乗法
次は多項式と多項式の乗法を見ていきましょう。分配が必要な多項式同士を掛け算するには、どのようにすればよいでしょうか?
例.(4x+3)(2y+1)
このままだとどうやって計算したらいいのか分からないですが、片方のカッコを文字として置くと、上で計算したようにすることができます。
今回は\(4x+3\)の部分をAと置き、\(A(2y+1\)を分配していきましょう。
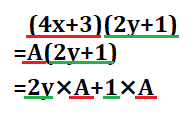
片方をAという文字で置いたことによって、このような形にすることができました。ここで、Aは\(4x+3\)なので、これを戻していきます。
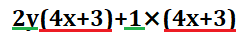
Aを\(4x+3\)に戻してみると、\(2y(4x+3)\)と\(1×(4x+3)\)が出てきました。これら2つは「単項式×多項式」の計算となるので、それぞれ展開していきます。
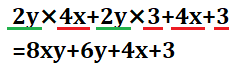
すると答えは
$$8xy+6y+4x+3$$
となります。
このように、カッコを外して、すべて単項式の和の形にすることを展開といいます。
一般的な場合を考えてみる
上の問題の答えでの項の数は4であることは見ただけで分かると思います。元々の式については(項2つ)×(項2つ)という形になっていますね。要するに、(項の数)×(項の数)=(展開される項の数)となることが分かります。(しかし、同類項がある場合は、その数以下になります。)
従って、このような多項式の展開は以下の式で表すことが出来ます。
$$(a+b)(c+d)=ac+ad+bc+bd$$
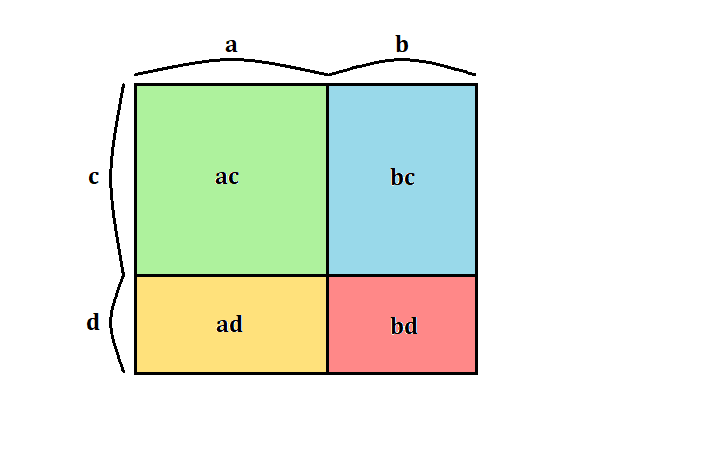
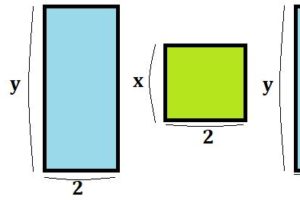
上の式を長方形の面積の図で示すとこのようになります。式で考えるのが難しい方は、図で考えてみるとわかりやすいかもしれません。
項が2以上の多項式を含む計算
例.(a+b+c)(d+e)
項が3つの多項式であっても、分配して計算することに変わりありません。
それぞれの項の組み合わせについて展開して計算すれば解くことが出来ます。
$$(a+b+c)(d+e)$$
$$=(a+b+c)d+(a+b+c)e$$
$$=ad+bd+cd+ae+be+ce$$
まとめ
- 単項式と多項式の乗算は、数と多項式の乗算と変わらず、多項式を分配して足し合わせる!
- 多項式同士の掛け算は、項同士のすべての組み合わせで掛け合わせる!
やってみよう
次の式を展開してみよう
- \(6a(3x+2y+4)\)
- \((5x+2)(3y-2)\)
- \((2x-1)(3x+4y-5)\)
こたえ
- \(18ax+12ay+24a\)
- \(15xy-10x+6y-4\)
- \(6x^{2}+8xy-13x-4y+5\)
解説:それぞれ\(6a×3x\)、\(6a×2y\)、\(6a×4\)で計算すると、\(18a\)、\(12ay\)、\(24\)となる。
解説:\((5x+2)\)を\(A\)とおく。\(A(3y-2)\)を計算すると\(3yA\)、\(-2A\)となる。Aを\((5x+2)\)に戻すと\(3y(5x+2)\)、\(-2(5x+2)\)となる。これを展開すると\(3y×5x\)、\(3y×2\)、\(-2×5x\)、\(-2×2\)となる。これを計算すると上記の答えとなる。
解説:\((2x-1)\)を\(A\)とおくと、\(A(3x+4y-5)\)となる。これを展開するとそれぞれ\(A×3x\)、\(A×4y\)、\(A×(-5)\)となる。Aを\((2x-1)\)に戻すと\((2x-1)(3x)\)、\((2x-1)4y\)、\((2x-1)(-5)\)となる。これを計算すると上記の答えとなる。
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。