こんにちは、家庭教師のあすなろスタッフのカワイです。
今回は、\(y=ax^{2}\)という関数の変域について解説していきたいと思います!
変域というのは、簡単に言うと、「ある一方の変数の動く範囲が決まっているときに、もう一方の変数の動ける範囲」のことでした。これを一次関数のときとの違いをしっかり確認してから、実際に今回のこの関数でどのように考えればいいのか、という流れで進めていきます!
\(y=ax^{2}\)についてまだよく分からないと思っている人や、\(y=ax^{2}\)のグラフがよく分からないという人でも進められるように、本編の前に復習できるようにしています。よろしければ最後まで読んでみて下さい!
それでは、今回も頑張っていきましょう!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書の採択を参考に中学校3年生のつまずきやすい単元の解説を行っています。
=もくじ=
【復習】\(y=ax^{2}\)とは?
\(y=ax^{2}\)とは、\(y\)が\(x\)の2乗に比例する関数です。
今まで勉強してきた\(y=ax\)では、\(x\)の値が1つ増えた時の\(y\)の増える量は一定でしたが、\(y=ax^{2}\)という式になると、\(x\)がどの値の時に1増えるかによって、\(y\)の増える量が変わるという特徴があります。
例えば、斜面を転がるボールの位置・時間を推測することが出来たりします。他にも様々な所で使われている関数です。
詳しくは→【中3数学】y=ax^2ってなに?y=ax^2が使われている例を解説します!
【復習】\(y=ax^{2}\)のグラフってどんな形をしているの?
\(y=ax^{2}\)のグラフは一次関数のような線形ではなく、放物線とよばれる曲線を描きます。
また、グラフの概形の最も下の部分もしくは最も上の部分が原点(\(x,y\))=(\(0,0\))を通り、いずれの場合も頂点といいます。
下のグラフが\(y=3x^{2}\)です。
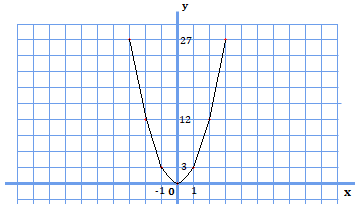
一方、下のグラフが\(y=-3x^{2}\)です。
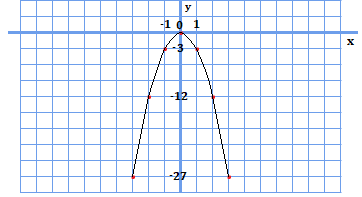
このように、係数\(a\)が正のときは上が開いた形に、負のときは下が開いた形となります。
より詳しく知りたい方は→【中3数学】y=ax^2のグラフってどんな形になるの?いくつかの特徴について解説!
\(y=ax^{2}\)の変域を考えてみよう。
では、早速本題に入っていきましょう。そのそも変域というのは、冒頭で紹介したように「ある一方の変数の動く範囲が決まっているときに、もう一方の変数の動ける範囲」のことです。これは今まで習ってきたどの関数でも考えられることなので、まず一次関数の場合を考えてみようと思います。
一次関数の時は?
\(y=2x\)という関数が\(x=1\)から\(x=3\)まで動くときの\(y\)の変域について考えてみましょう。式からだとイメージするのが難しいので、まずグラフで\(y=2x\)を表してみます。
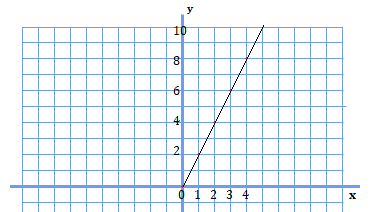
見慣れた直線のグラフですね。このグラフにおいて\(x=1\)と\(x=3\)を示すと、
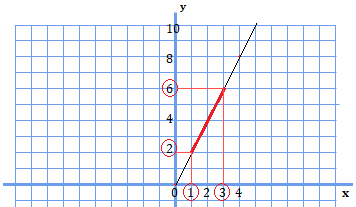
となります。\(x=1\)のときの\(y\)は\(2\)、\(x=3\)のときの\(y\)は\(6\)となり、その間の\(y\)の値は\(2\)よりも大きく\(6\)よりも小さくなっています。グラフを見たら明らかですね。
従って、変域は\(2≦y≦6\)となります。
さて、このような考え方を踏まえて、\(y=ax^{2}\)の形の問題を考えてみましょう。
例1.\(y=x^{2}\)について、\(x\)の変域が\(1≦x≦3\)の時の\(y\)の変域を求めよう。
一次関数の例と同じように、まず関数をグラフに表していきます。
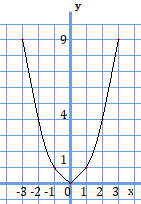
次に、変域の端の値である\(x=1\)と\(x=3\)の時の\(y\)の値を考えてみます。
関数\(y=x^{2}\)に\(x=1\)と\(x=3\)を代入すると、\(x=1\)のとき\(y=1\)、\(x=3\)のとき\(y=9\)となっています。
グラフより経路を考えてみると、
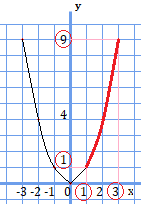
となっており、\(y=1\)が一番小さい値、\(y=9\)が一番大きい値となっていることが分かります。
従って、\(y=x^{2}\)の\(x\)の変域が\(1≦x≦3\)の時、\(y\)の変域は\(1≦y≦9\)となります。
例2.\(y=x^{2}\)について、\(x\)の変域が\(-3≦x≦2\)の時の\(y\)の変域を求めよう。
次の関数も同じように\(y=x^{2}\)の変域について考えてみます。グラフは例1と同様なので割愛しますね。
次に、変域の端の値である\(x=-3\)と\(x=2\)の時の\(y\)の値を考えてみます。
関数\(y=x^{2}\)に\(x=-3\)と\(x=2\)を代入すると、\(x=-3\)のとき\(y=9\)、\(x=2\)のとき\(y=4\)となっています。
さて、これまで\(x\)の変域の端のときの\(y\)の値が\(y\)の変域の端だったので、
変域は\(4≦y≦9\)となります。
と言いたいところですが、これは間違いです!
\(y=ax^{2}\)の特徴をよく覚えている人だったら分かるかもしれません。さて、グラフを見てみましょう。
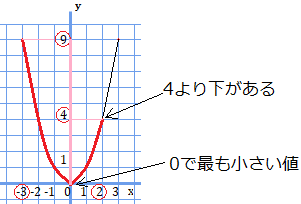
\(y=9\)は確かに一番大きな値となっています。一方で\(y=4\)はどうでしょうか。\(x\)の変域での\(y\)の変域を考えると、\(y=4\)を下回って、\(y=0\)まで来ているではありませんか。
変域を考えるときは、移動した値すべての中で、どこが一番値が大きい・小さいところをとるので、この場合\(y=4\)は変域とは関係のない値となります。
従って、今回の変域の正解は\(0≦y≦9\)です。
何故かは、グラフを見て分かったかと思いますが、\(y=ax^{2}\)は\(x=0\)で\(y=0\)となり、一番低い値をとるからです。
そして、\(x\)の符号によらず、絶対値によって\(y\)の値が決まる(例えば\(x=10\)の時と\(x=-10\)の時の\(y\)の値は同じ)ので、\(x=-3\)と\(x=2\)では\(x=-3\)の時の方が\(y\)の値が大きくなります。
例1と例2を踏まえ、ここで軽くまとめてみると、
\(y=ax^{2}\)(グラフの形が下に凸)のとき
\(x\)の変域が原点を通らない場合
- 一次関数と同様に「\(x\)の変域の端の値」のとき「\(y\)の変域の端の値」となる。
\(x\)の変域が原点を通る場合
- 原点が\(y\)の変域のうち一番小さい値となり、「\(x\)の変域の端のうち絶対値が大きい方」の\(y\)の値が一番大きい値となる。
例3.\(y=-x^{2}\)について、\(x\)の変域が\(-1≦x≦2\)の時の\(x\)の変域を求めよう。
最後に、\(y=-x^{2}\)の変域について考えてみましょう。
まず、グラフを考えてみると、
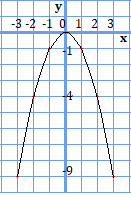
となります。先程の\(y=x^{2}\)とは違い、上に凸の関数になっています。さて、\(x=-1\)から\(x=2\)までの\(y\)の値の動きをグラフ上で考えていこうと思います。
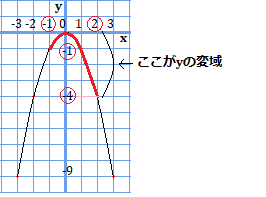
グラフの見た目より、\(x=2\)の値が\(y=-4\)となっており、最も小さくなっています。
一方、最も大きくなっている点は\(x=-1\)かというと、そうではなく\(x=0\)となっていますね。
これは例2で解説したことと同じですが、このグラフは\(x=0\)を頂点として上に凸となっているので、\(x=0\)をまたぐ変域の場合は、\(y=0\)が最大の値となります。
これについてまとめてみると、
\(y=ax^{2}\)(グラフの形が下に凸)のとき
\(x\)の変域が原点を通らない場合
- 一次関数と同様に「\(x\)の変域の端の値」のとき「\(y\)の変域の端の値」となる。
\(x\)の変域が原点を通る場合
- 原点が\(y\)の変域のうち一番大きいとなり、「\(x\)の変域の端のうち絶対値が大きい方」の\(y\)の値が一番小さい値となる。
まとめ
最後に、もう一度まとめてしめようと思います。
\(y=ax^{2}\)(グラフの形が下に凸)のとき
\(x\)の変域が原点を通らない場合
- 一次関数と同様に「\(x\)の変域の端の値」のとき「\(y\)の変域の端の値」となる。
\(x\)の変域が原点を通る場合
- 原点が\(y\)の変域のうち一番小さい値となり、「\(x\)の変域の端のうち絶対値が大きい方」の\(y\)の値が一番大きい値となる。
\(y=ax^{2}\)(グラフの形が上に凸)のとき
\(x\)の変域が原点を通らない場合
- 一次関数と同様に「\(x\)の変域の端の値」のとき「\(y\)の変域の端の値」となる。
\(x\)の変域が原点を通る場合
- 原点が\(y\)の変域のうち一番大きいとなり、「\(x\)の変域の端のうち絶対値が大きい方」の\(y\)の値が一番小さい値となる。
僕が今回の「\(y=ax^{2}\)の変域」の解説で伝えたいことは、「グラフを活用して解こう!」ということです。式だけを眺めていると、変域として書かれている値をそのまま代入したら答えが出せると思いがちになってしまいますが、それは一次関数までで、\(y=ax^{2}\)に関してはそうはいかない事が多いです。
まとめの中で要点を書きはしましたが、グラフを書いて考えれば絶対に間違えない問題だと思うので、是非グラフを書くことをクセにして解いてみましょう!(分かるようになったら書かなくてもいいと思います。)
やってみよう!
- \(y=3x^{2}\)の\(x\)の変域が以下のときの、\(y\)の変域を求めてみよう。
- \(-3≦x≦-1\)
- \(-2≦x≦3\)
- \(y=-2x^{2}\)の\(x\)の変域が以下のときの、\(y\)の変域を求めてみよう。
- \(1≦x≦4\)
- \(-2≦x≦1\)
こたえ
-
- \(3≦y≦27\)
- \(0≦y≦27\)
-
- \(-32≦y≦-2\)
- \(-8≦y≦0\)
最後までご覧いただきありがとうございました。
「数学でわからないところがある」そんな時に役立つのが、勉強お役立ち情報!
数学の単元のポイントや勉強のコツをご紹介しています。
ぜひ参考にして、テストの点数アップに役立ててみてくださいね。
もし上記の問題で、わからないところがあればお気軽にお問い合わせください。少しでもお役に立てれば幸いです。