こんにちは、あすなろスタッフのカワイです。
反比例は比例とは違い、グラフの形が異なっていたり、一方の変数を\(2\)倍にすると、もう一方の変数が\(\frac{1}{2}\)倍となることなどを、図形の辺と面積の関係の例を用いて前回解説しました。
今回はその続きですが、グラフの範囲を拡張したり、比例定数が負になる場合について、なるべく簡単に解説していきたいと思います!では、頑張っていきましょう。
関連記事:【中1数学】反比例の式と性質、グラフについて簡単に解説します!
あすなろには、毎日たくさんのお悩みやご質問が寄せられます。
この記事は数学の教科書に基づいて中学校1年生のつまずきやすい単元の解説を行っています。
文部科学省 学習指導要領「生きる力」
=もくじ=
反比例の1つの式からグラフが2本できる!?
前回の解説記事のお話では、反比例のグラフは1つしか出てきませんでした。式1つに対してグラフが1つ出来るのは違和感ありませんよね。しかしながら、場合によってはグラフが2つ現れるのです。
どういうことなのか、解説していきます。
例1.\(y=\frac{20}{x}\)のグラフを示そう。
この式を見ると、\(y=\frac{a}{x}\)の形になっているので、これは反比例の関数であると分かります。このグラフを示すために、まず表を作成してみましょう。
表にするにあたって、20の約数を示してみると、
$$1,2,4,5,10,20$$
となるので、その値から表を作成していきます。
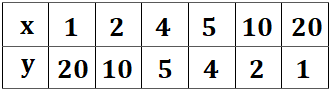
このように表が出来ました。が、これでは不十分です。何故かというと…負の数の範囲を考えていないからです。
仮に\(x=-1\)を代入すると、
$$y=\frac{20}{-1}$$
より、
$$y=-20$$
となります。これより、負の数の範囲にも値が存在しそうだな…と分かります。
何故負が存在するのか?
\(y=\frac{20}{x}\)は\(xy=20\)と書き換えることが出来ます。要するに、反比例というのは、掛け算の積だけが決まっていて、実際の式のほうが決まっていない状態ということができるわけです。
\(x\)と\(y\)の積が正の数となる場合を考えたとき、
- (正の数)×(正の数)=(正の数)
- (負の数)×(負の数)=(正の数)
の2通りが考えられます。従って、このように正の場合と負の場合の両方を考えなければならないのです。
前回の記事では、図形という正の範囲での話であったために、負の値について明示しませんでしたが、このように範囲の指定がない場合は、基本的に負の範囲も考える必要があります。
先程出した約数の値を負の範囲にも拡張して表を作成してみます。
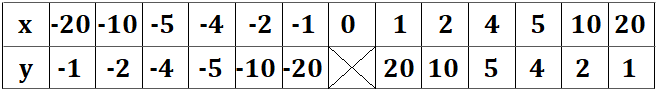
\(x\)が\(0\)は存在しないので、×をうちました。\(0\)が存在せず、でも正負両方の値が存在する…どんなグラフになるのでしょうか。下に示してみます。
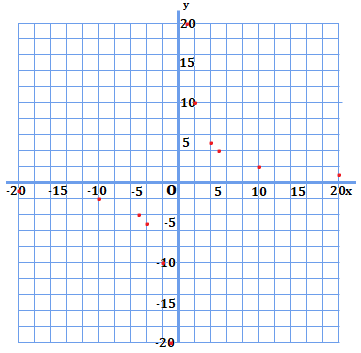
正と負の両範囲に値がありますが、比例のグラフとは異なり、1つの線で表すのが難しそうです(\(0\)が存在しない為)。ただし、正の範囲と負の範囲の2つと考えてみれば、弧を描くことが出来そうです。これらの点を曲線でつないでみます。
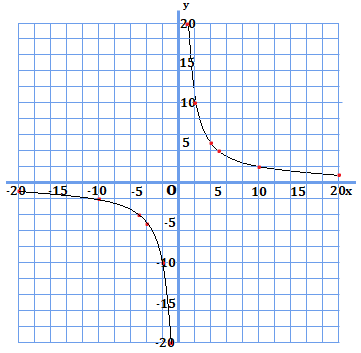
原点対称の図形が示されました。これが比例定数が正のときの反比例のグラフの形になります。
比例定数が負の場合はどうなるの?
前の場合は比例定数が正でしたが、比例定数が負の場合はどうなるのでしょうか。何となく予想は付きますが、考えていきましょう。
例2.\(y=\frac{-10}{x}\)のグラフを示そう。
グラフにする前に、表を作っていきたいですが、例1と同様に約数を考えてから表に代入する形で考えましょう。10の約数は、
$$1,2,5,10$$
となります。また、比例定数が負(=積が負)となる掛け算の正負の組み合わせを考えてみると
- (正の数)×(負の数)=(負の数)
- (負の数)×(正の数)=(負の数)
となります。従って、\(x\)と\(y\)の符号は常に逆となりそうです。
では、表を作成してみましょう!
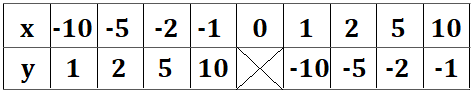
では、これをグラフに表してみましょう。
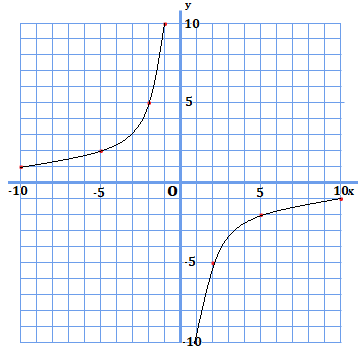
グラフに表すことが出来ました。このように、比例定数が負の場合は、正の場合と現れる場所が異なります。
まとめ
反比例の特徴
- 反比例のグラフのとき、比例定数が正の場合は右上と左下に、負の場合は左上と右下にそれぞれグラフが表される(範囲が実数の場合)。
今回は、反比例の双曲線が2本表されるということと、比例定数が正の場合と負の場合のグラフの位置が異なるという2点について解説しました。比例と反比例という似た名前なのに、性質が全く異なるので混乱するかもしれませんが、一つ一つ確実に抑えて勉強していきましょう。
次回は反比例のグラフから式を導出する方法を解説します。